题目内容
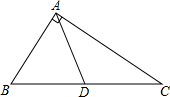 (1)如图,在△ABC中,AD是BC边上的中线,且AD=
(1)如图,在△ABC中,AD是BC边上的中线,且AD=| 1 |
| 2 |
(2)此题实际上是直角三角形的另一个判断定理,请你适当的方法表达出来.
(3)直接运用这个结论解答下面问题:在△ABC中,AD是BC边上的中线,BC=2,AD=1,AB+AC=1+
| 3 |
分析:(1)根据中线的定义可得AD=BD=DC,再根据等边对等角可得∠B=∠BAD,∠C=∠CAD,然后根据三角形内角和定理列式求解得到∠BAD+∠CAD=90°,从而得证;
(2)根据条件与结论写出即可;
(3)先求出∠BAC=90°,再根据勾股定理列式求出AB2+AC2,然后利用完全平方公式求出AB•AC,再根据三角形的面积公式列式计算即可得解.
(2)根据条件与结论写出即可;
(3)先求出∠BAC=90°,再根据勾股定理列式求出AB2+AC2,然后利用完全平方公式求出AB•AC,再根据三角形的面积公式列式计算即可得解.
解答:(1)证明:∵AD是BC边上的中线,
∴BD=CD,
∵AD=
BC,
∴AD=BD=DC,
∴∠B=∠BAD,∠C=∠CAD,
∵∠B+∠BAD+∠C+∠CAD=90°,
∴∠BAD+∠CAD=90°,
即∠BAC=90°;
(2)解:根据题意用语言表述为:如果三角形一条边上的中线等于这边的一半,那么这个三角形是直角三角形;
(3)∵AD是BC边上的中线,BC=2,AD=1,
∴∠BAC=90°,
由勾股定理得,AB2+AC2=BC2=22=4,
∵AB+AC=1+
,
∴AB2+2AB•AC+AC2=(1+
)2=4+2
,
∴AB•AC=
,
S△ABC=
AB•AC=
.
∴BD=CD,
∵AD=
| 1 |
| 2 |
∴AD=BD=DC,
∴∠B=∠BAD,∠C=∠CAD,
∵∠B+∠BAD+∠C+∠CAD=90°,
∴∠BAD+∠CAD=90°,
即∠BAC=90°;
(2)解:根据题意用语言表述为:如果三角形一条边上的中线等于这边的一半,那么这个三角形是直角三角形;
(3)∵AD是BC边上的中线,BC=2,AD=1,
∴∠BAC=90°,
由勾股定理得,AB2+AC2=BC2=22=4,
∵AB+AC=1+
| 3 |
∴AB2+2AB•AC+AC2=(1+
| 3 |
| 3 |
∴AB•AC=
| 3 |
S△ABC=
| 1 |
| 2 |
| ||
| 2 |
点评:本题考查了勾股定理,三角形的内角和定理,直角三角形斜边上的中线等于斜边的一半的性质与判定,等腰三角形的性质,完全平方公式,理解题意并证明出直角三角形的判定定理是解题的关键,也是本题的难点.

练习册系列答案
相关题目
 16、如图,在①AB=AC ②AD=AE ③∠B=∠C ④BD=CE四个条件中,能证明△ABD与△ACE全等的条件顺序是( )
16、如图,在①AB=AC ②AD=AE ③∠B=∠C ④BD=CE四个条件中,能证明△ABD与△ACE全等的条件顺序是( ) 34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2, 16、如图,在AB、AC上各取一点D、E,使得AE=AD,连接CD、BE相交于点O,再连接AO.若∠CAO=∠BAO,则图中全等三角形共有( )
16、如图,在AB、AC上各取一点D、E,使得AE=AD,连接CD、BE相交于点O,再连接AO.若∠CAO=∠BAO,则图中全等三角形共有( ) 18、如图,在AB∥CD,∠A=40°,∠C=80°.求∠E的度数.
18、如图,在AB∥CD,∠A=40°,∠C=80°.求∠E的度数. 如图,在AB、AC上各取一点E、D,使AE=AD,连接BD、CE相交于点O,再连接AO、BC,若∠1=∠2,则图中全等三角形共有( )
如图,在AB、AC上各取一点E、D,使AE=AD,连接BD、CE相交于点O,再连接AO、BC,若∠1=∠2,则图中全等三角形共有( )