题目内容
如图，一艘轮船以15海里/时的速度由南向北航行，上午8时，在A处测得小岛P在西偏北75°的方向上，10时到达B处，轮船在B处测得小岛P在北偏西30°的方向上，则从B处到小岛P的距离是多少？
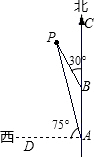
依题意得：AB=15×（10-8）=30（海里）．
∵∠PAB=∠CAD-∠PAD=90°-75°=15°，
∠PBC=30°，
∴∠P=∠PBC-∠PAB=15°，
∴∠P=∠PAB，
∴PB=AB=30（海里）．
∴从B处到小岛P的距离是30海里．
∵∠PAB=∠CAD-∠PAD=90°-75°=15°，
∠PBC=30°，
∴∠P=∠PBC-∠PAB=15°，
∴∠P=∠PAB，
∴PB=AB=30（海里）．
∴从B处到小岛P的距离是30海里．
练习册系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
