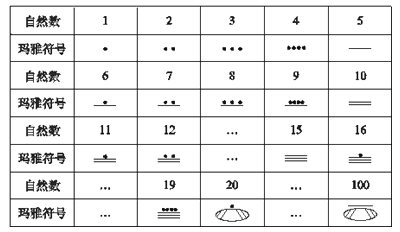
题目内容
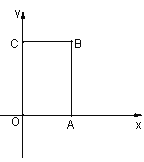
【题目】如图，在长方形OABC中，O为平面直角坐标系的原点，OA=4，AB=6,点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动．
（1）点B的坐标为 ；
（2）当点P移动4秒时，请指出点P的位置，并求出点P的坐标.
【答案】（1)（4，6）；（2）当点P移动4秒时，此时点P在线段CB上，点P的坐标是（2，6）.
【解析】试题分析：（1）根据OA、AB的长以及矩形即可得；
（2）按点P的运动速度以及运动的时间即可确定.
试题解析：（1）∵四边形OABC是矩形，OA=4，AB=6，∴点B的坐标是（4，6）；
（2）∵点P从原点出发，以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动，∴2×4=8，
∵OA=4，OC=6，∴当点P移动4秒时，在线段CB上，离点C的距离是：8﹣6=2，
即当点P移动4秒时，此时点P在线段CB上，离点C的距离是2个单位长度，点P的坐标是（2，6）.
练习册系列答案
相关题目
