Question

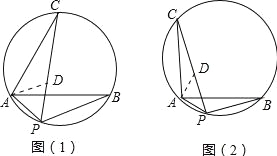
【题目】如图（1），将线段AB绕点A逆时针旋转2α（0°＜α＜90°）至AC，P是过A，B，C的三点圆上任意一点．

（1）当α=30°时，如图（1），求证：PC=PA+PB；

（2）当α=45°时，如图（2），PA，PB，PC三条线段间是否还具有上述数量关系？若有，请说明理由；若不具有，请探索它们的数量关系．

Answer 1

【答案】(1)证明详见解析；(2)PC=PA+PB，理由详见解析.

【解析】

试题分析：（1）首先在PC上截取PD=PA，易知△ABC是等边三角形，可得△PAD是等边三角形，继而可证明△ACD≌△BAP，则CD=PB，从而得出PC=PB+PA；

（2）PC=PA+PB，作AD⊥AP与PC交于一点D，易证△ACD≌△ABP，则CD=PB，AD=AP，根据勾股定理PD=PA，所以PC=PA+PB．

试题解析：证明：（1）如图（1），在PA上截取PD=PA，

∵AB=AC，∠CAB=60°，

∴△ABC为等边三角形，

∴∠APC=∠CPB=60°，

∴△APD为等边三角形，

∴AP=AD=PD，

∴∠ADC=∠APB=120°，

在△ACD和△ABP中，

∠ADC=∠APB，∠ACD=∠ABP，AD=AP，

∴△ACD≌△ABP（AAS），

∴CD=PB，

∵PC=PD+DC，

∴PC=PA+PB；

（2）PC=PA+PB，；理由如下：

如图（2），作AD⊥AP与PC交于一点D，

∵∠BAC=90°，

∴∠CAD=∠BAP，

在△ACD和△ABP中，

∠CAD=∠BAP，AC=AB，∠ACD=∠ABP，

∴△ACD≌△ABP，

∴CD=PB，AD=AP，

根据勾股定理PD=PA，

∴PC=PD+CD=PA+PB．