题目内容
【题目】我们知道,如果两个三角形全等,则它们面积相等,而两个不全等的三角形,在某些情况下,可通过证明等底等高来说明它们的面积相等.已知△ABC与△DEC是等腰直角三角形,∠ACB=∠DCE=90°,连接AD、BE. 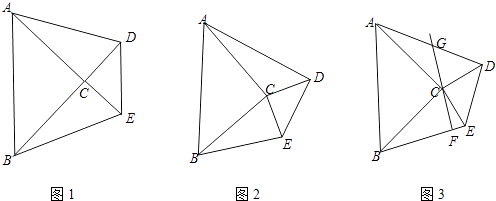
(1)如图1,当∠BCE=90°时,求证:S△ACD=S△BCE;
(2)如图2,当0°<∠BCE<90°时,上述结论是否仍然成立?如果成立,请证明;如果不成立,说明理由.
(3)如图3,在(2)的基础上,作CF⊥BE,延长FC交AD于点G,求证:点G为AD中点.
【答案】
(1)证明:∵△ABC与△DEC是等腰直角三角形,
∴AC=BC,DC=EC,∠ACB=∠DCE
∵∠BCE=90°,
∴∠ACE=∠BCE,
在△ACD与△BCE中,
 ,
,
∴△ACD≌△BCE(SAS),
∴S△ACE=S△BCE
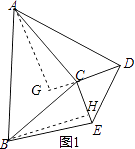
(2)证明:作AG垂直DC的延长线于点G,作BH⊥CE,垂足为H,
∵∠ACB=∠GCE=90°,
∴∠ACG=∠BCH,
在△ACG与△BCF中,
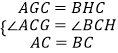 ,
,
∴△ACG≌△BCH(AAS)
∴AG=BH
∵CD=CE
∴ ![]() CDAG=
CDAG= ![]() CEBH,
CEBH,
即S△ACE=S△BCE
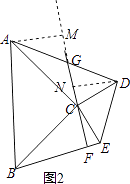
(3)证明:作AM垂直CG的延长线于点M,作DN⊥CG,垂足为N,
∴∠ACB=90,∠BFC=90°,
∴∠ACM+∠BCF=90°,∠BCF+∠CBF=90°,
∴∠ACM=∠CBF,
在△ACM与△BCF中,
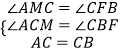 ,
,
∴△ACM≌△CBF(AAS),
∴AM=CF,
同理可证△DCN≌△CEF,
∴DN=CF,
∴AM=DN,
又∵∠AMG=∠DNG,
∴∠AGM=∠DGN,
在△AMG与△DNG中,
 ,
,
∴△AMG≌△DNG(AAS),
∴AG=DG,
即G为AD中点,
【解析】(1)根据△ABC与△DEC是等腰直角三角形,得到AC=BC,DC=EC,∠ACB=∠DCE由∠BCE=90°,证得∠ACE=∠BCE,推出△ACD≌△BCE,从而证得结论S△ACE=S△BCE;(2)作AG垂直DC的延长线于点G,作BH⊥CE,垂足为H,由于∠ACB=∠GCE=90°,得到∠ACG=∠BCH,推出△ACG≌△BCH,得出AG=BH,由于CD=CE,于是得到结果即S△ACE=S△BCE;(3)作AM垂直CG的延长线于点M,作DN⊥CG,垂足为N,证得△ACM≌△CBF,得到AM=CF,同理可证△DCN≌△CEF,得到DN=CF,AM=DN,推出△AMG≌△DNG,得到AG=DG,即G为AD中点.
【考点精析】本题主要考查了等腰直角三角形的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能正确解答此题.