题目内容
【题目】如图，正方形
中，
，点
为
的中点，点
在
上，且
，点
为直线
上一动点，
的最大值是_________．
【答案】
【解析】
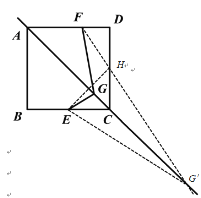
取CD的中点H，根据题意可知点E,H关于AC对称，连接FH并延长交直线AC于一点G′，连接EG,则EG′=HG′，此时FG′-EG′=FH，FH即为FG-EG的最大值.
解：取CD的中点H，
∵四边形ABCD为正方形，点E 为BC中点，
∴易得点E,H关于AC对称，
连接FH并延长交直线AC于一点G′，连接EG′,根据对称性可知EG′=HG′，
此时FG′-EG′=FH，
根据三角形中两边之差小于第三边可知，FH为FG-EG的最大值.
又∵DF=2，AB=CD=6，H为CD中点，∴DH=3，
在Rt△DFH中，根据勾股定理可得，FH=
.
即FG-EG的最大值为.
故答案为：.
练习册系列答案
相关题目
