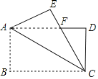
题目内容
【题目】如图,从![]() 外一点
外一点![]() 引圆的两条切线
引圆的两条切线![]() 、
、![]() ,切点为
,切点为![]() 、
、![]() ,点
,点![]() 是劣弧
是劣弧![]() 上一点,过
上一点,过![]() 的切线交
的切线交![]() 、
、![]() 分别于
分别于![]() 、
、![]() ,若
,若![]() 的半径为
的半径为![]() ,
,![]() ,则
,则![]() 的周长为( )
的周长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
连接OP,由圆外一点P作圆的两条切线PA与PB,根据切线长定理得到PA=PB,且PO为角平分线,由∠APB=60°,得到∠APO=30°,再由切线的性质得到OA与AP垂直,在直角三角形APO中,根据30°角所对的直角边等于斜边的一半,由半径OA的长求出斜边OP的长,再利用勾股定理求出AP的长,由MA与MC为圆O的切线,根据切线长定理得到MA=MC,同理可得NB=NC,然后把三角形PMN的三边相加表示出三角形PMN的周长,等量代换后得到其周长为2PA,把PA的长代入即可求出三角形PMN的周长.
连接OP.
∵PA,PB为圆O的切线,∴PA=PB,PO平分∠APB,OA⊥AP.
又∵∠APB=60°,∴∠APO=30°,在直角三角形APO中,OA=2,∴OP=2OA=4,根据勾股定理得:PA=![]() =2
=2![]() .
.
∵MA,MC为圆O的两条切线,∴MA=MC,又NB,NC为圆O的切线,∴NC=NB,∴△PMN的周长=PM+PN+MN=PM+PN+MC+NC=PM+PN+MA+NB=PA+PB=2PA=4![]() .
.
故选C.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目