题目内容
【题目】(1)如图1,矩形ABCD的对角线AC、BD交于点O,过点C作BD的平行线,过点D作AC的平行线,两线交于点P,则四边形CODP的形状是 ;
(2)如图2,若题目中的矩形变为菱形,则四边形CODP的形状是 ;
(3)如图3,若题目中的矩形变为正方形,请判断四边形CODP的形状,并说明理由.

【答案】(1)四边形CODP的形状是菱形,理由见解析;(2)四边形CODP的形状是矩形,理由见解析;(3)四边形CODP的形状是正方形,理由见解析
【解析】
(1)根据矩形的性质得出OD=OC,根据有一组对边平行且相等的四边形是平行四边形得出四边形CODP是平行四边形,根据菱形的判定推出即可;
(2)根据菱形的性质得出∠DOC=90°,根据有一组对边平行且相等的四边形是平行四边形得出四边形CODP是平行四边形,根据矩形的判定推出即可;
(3)根据正方形的性质得出OD=OC,∠DOC=90°,根据有一组对边平行且相等的四边形是平行四边形得出四边形CODP是平行四边形,再根据正方形的判定推出即可.
(1)如图1,四边形CODP的形状是菱形,
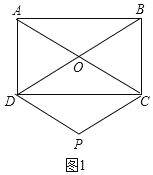
理由是:∵四边形ABCD是矩形,
∴AC=BD,OA=OC=![]() AC,OB=OD=
AC,OB=OD=![]() BD,
BD,
∴OC=OD,
∵DP∥OC,DP=OC,
∴四边形CODP是平行四边形,
∵OC=OD,
∴平行四边形CODP是菱形;
(2)如图2,四边形CODP的形状是矩形,
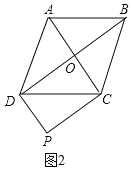
理由是:∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∵DP∥OC,DP=OC,
∴四边形CODP是平行四边形,
∵∠DOC=90°,
∴平行四边形CODP是矩形;
故答案为:矩形;
(3)四边形CODP的形状是正方形,
理由是:∵四边形ABCD是正方形,
∴AC⊥BD,AC=BD,OA=OC=![]() AC,OB=OD=
AC,OB=OD=![]() BD,
BD,
∴∠DOC=90°,OD=OC,
∵DP∥OC,DP=OC,
∴四边形CODP是平行四边形,
∵∠DOC=90°,OD=OC
∴平行四边形CODP是正方形.
故答案为:正方形.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案