��Ŀ����
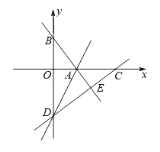
����Ŀ����ͼ����֪һ�κ���y=![]() x+m��ͼ����x�ύ�ڵ�A����4��0��������κ���y=ax2+bx+c��ͼ����y����һ��B���ö��κ����Ķ���C��x���ϣ���OC=2��
x+m��ͼ����x�ύ�ڵ�A����4��0��������κ���y=ax2+bx+c��ͼ����y����һ��B���ö��κ����Ķ���C��x���ϣ���OC=2��
��1�����B���ꣻ
��2������κ���y=ax2+bx+c�Ľ���ʽ��
��3����һ�κ���y=![]() x+m��ͼ������κ���y=ax2+bx+c��ͼ�����һ����ΪD����֪PΪx���ϵ�һ�����㣬�ҡ�PBD����BDΪֱ�DZߵ�ֱ�������Σ����P�����꣮
x+m��ͼ������κ���y=ax2+bx+c��ͼ�����һ����ΪD����֪PΪx���ϵ�һ�����㣬�ҡ�PBD����BDΪֱ�DZߵ�ֱ�������Σ����P�����꣮

���𰸡���1��B��0��2������2��y=0.5x2��2x+2����3��P1��1��0����P2��7.25��0����
��������
��1������y=0.5x+m��x���ڵ�A�������ó�m��ֵ����������y�ύ�ڵ�B�����ɵó�B�����ꣻ��2�����κ���y=ax2+bx+c��ͼ����x��ֻ��Ψһ�Ľ���C����OC=2���ó�������κ���y=ax2+bx+c=a��x��2��2������������ɣ���3�����ݵ�BΪֱ�Ƕ��㣬��DΪֱ�Ƕ���ʱ���ֱ��������������ƶ�Ӧ�߳ɱ���������ɣ�
��1����y=![]() x+2��x���ڵ�A����4��0����
x+2��x���ڵ�A����4��0����
��0=![]() ������4��+m��
������4��+m��
��m=2��
��y�ύ�ڵ�B��
��x=0��
��y=2
��B����������0��2����
��2���߶��κ���y=ax2+bx+c��ͼ����x��ֻ��Ψһ�Ľ���C����OC=2
���������y=a��x��2��2
��B��0��2������ã�a=0.5
����κ����Ľ���ʽ��y=0.5x2��2x+2��
��3������BΪֱ�Ƕ���ʱ����B��BP1��AD��x����P1��
��Rt��AOB��Rt��BOP1
��![]() ��
��
��![]() ��
��
�ã�OP1=1��
��P1��1��0����
������P2D��BD������BP2��
��y=0.5x+2��y=0.5x2��2x+2��������������������꣺
D����������5��4.5����
��AD=![]() ��
��
��DΪֱ�Ƕ���ʱ
�ߡ�DAP2=��BAO����BOA=��ADP2��
���ABO�ס�AP2D��
��![]() ��
��![]() ��
��
��ã�AP2=11.25��
��OP2=11.25��4=7.25��
��P2��������7.25��0����
���P��������P1��1��0����P2��7.25��0����

 ��У����ϵ�д�
��У����ϵ�д�