题目内容
【题目】已知：甲、乙两车分别从相距300千米的A，B两地同时出发相向而行，甲到B地后立即返回，下图是它们离各自出发地的距离y（千米）与行驶时间x（小时）之间的函数图象．
（1）请直接写出甲、乙两车离各自出发地的距离y（千米）与行驶时间x（小时）之间的函数关系式，并标明自变量x的取值范围；
（2）它们在行驶的过程中有几次相遇？并求出每次相遇的时间．
【答案】
（1）解：甲由3小时到 
小时的速度是： 
=80千米/小时．
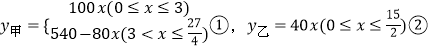
（2）解：由题意有两次相遇．
方法一：①当0≤x≤3时，100x+40x=300，解得 
，
②当 
时，（540﹣80x）+40x=300，解得x=6，
综上所述，两车第一次相遇时间为第 
小时，第二次相遇时间为第6小时．
方法二：设经过x小时两车首次相遇，
则40x+100x=300，解得 ，
设经过x小时两车第二次相遇，
则80（x﹣3）=40x，解得x=6．
综上所述，两车第一次相遇时间为第 小时，第二次相遇时间为第6小时．
【解析】（1）依图可知y甲的函数关系式为分段函数，y乙=40x，并标明自变量x的取值范围；
（2）如图可知甲与乙有两次相遇．再分段列方程求解即可得到答案．
练习册系列答案
相关题目
【题目】某某摩托车厂本周计划每日生产
辆摩托车，由于工人实行轮休，每日上班人数不一定相等，实际每日生产量，与计划量相比情况如下表（增加的车辆数为正数，减少的车辆数为负数）
根据记录回答：
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
（1）本周三生产了多少摩托车？
（2）本周总生产量与计划生产量相比，是增加还是减少？
（3）产量最多的一天比产量最少的一天多生产了多少辆？
