题目内容
【题目】如图,已知矩形![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上一动点,
上一动点,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点.
的中点.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)当![]() 为何值时,四边形
为何值时,四边形![]() 是菱形,说明理由.
是菱形,说明理由.
(3)四边形![]() 有可能是矩形吗?若有可能,求出
有可能是矩形吗?若有可能,求出![]() 的长;若不可能,请说明理由.
的长;若不可能,请说明理由.
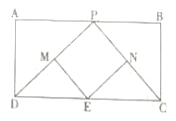
【答案】(1)见解析(2)当![]() 时,四边形
时,四边形![]() 是菱形(3)当
是菱形(3)当![]() 或
或![]() 时,四边形
时,四边形![]() 是矩形
是矩形
【解析】
(1)根据三角形的中位线的性质和平行四边形的判定定理可证明;
(2)当P是AB的中点时,四边形PMEN是菱形,所以可求出AP的值;
(3)四边形PMEN是矩形的话,∠DPC必需为90°,判断一下△DPC是不是直角三角形就行.
(1)![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点,
的中点,
![]() 是
是![]() 的中位线,
的中位线,![]() 是
是![]() 的中位线,
的中位线,
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形;
是平行四边形;
(2)当![]() 时,四边形
时,四边形![]() 是菱形,
是菱形,
理由如下:
当![]() 时,即
时,即![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
![]() ,
,
![]() ,
,
![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点,
的中点,
![]() ,
,![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是菱形;
是菱形;

(3)四边形![]() 可能是矩形.
可能是矩形.
若四边形![]() 是矩形,则
是矩形,则![]() ,
,
设![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 或
或![]() .
.
故当![]() 或
或![]() 时,四边形
时,四边形![]() 是矩形.
是矩形.

练习册系列答案
相关题目
【题目】已知y=ax2+bx+c(其中a,b,c为常数,且a≠0),乐老师在用描点法画其的图象时,列出如下表格,根据该表格,下列判断中不正确的是( )
x | … | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣2 | 2.5 | 4 | 2.5 | … |
A. a<0
B. 一元二次方程ax2+bx+c﹣5=0没有实数根
C. 当x=3时y=﹣2
D. 一元二次方程ax2+bx+c=0有一根比3大