题目内容
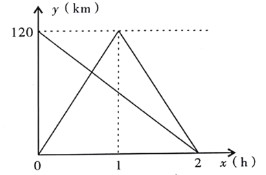
【题目】甲、乙两人参加从A地到B地的长跑比赛，两人在比赛时所跑的路程y（米）与时间x（分钟）之间的函数关系如图所示，请你根据图象，回答下列问题：
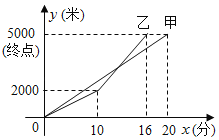
（1） 先到达终点（填“甲”或“乙”）；甲的速度是 米/分钟；
（2）甲与乙何时相遇？
（3）在甲、乙相遇之前，何时甲与乙相距250米？
【答案】（1）乙；250米/分钟；（2）12分钟时相遇；（3）5分钟时
【解析】
（1）依据函数图象可得到两人跑完全程所用的时间，从而可知道谁先到达终点，依据速度＝路程÷时间可求得甲的速度；
（2）先求得甲的路程与时间的函数关系式，然后求得10＜x＜16 时，乙的路程与时间的函数关系式，最后，再求得两个函数图象交点坐标即可；
（3）根据题意列方程解答即可．
解：（1）由函数图象可知甲跑完全程需要20分钟，乙跑完全程需要16分钟，所以乙先到达终点；
甲的速度＝
＝250 米/分钟．
故答案为：乙；250．
（2）设甲跑的路程y（米）与时间x（分钟）之间的函数关系式为y＝kx，
根据图象，可得y＝
x＝250x，
设10分钟后（即10＜x＜16 ），乙跑的路程y（米）与时间x（分钟）之间的函数关系式为：y＝kx+b．
根据图象，可得
，
解得
，
所以10分钟后乙跑的路程y（米）与时间x（分钟）之间的函数关系式
，
联立甲乙两人的函数关系式
解得
，
答：甲与乙在12分钟时相遇；
（3）设此时起跑了x分钟，
根据题意得
，
解得x＝5．
答：在甲、乙相遇之前，5分钟时甲与乙相距250米．
练习册系列答案
相关题目
