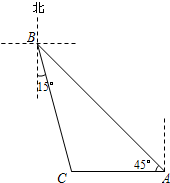
题目内容
九（1）班的数学课外小组，对公园人工湖中的湖心亭A处到笔直的南岸的距离进行测量．他们采取了以下方案：如图，站在湖心亭的A处测得南岸的-尊石雕C在其东南方向，再向正北方向前进10米到达B处，又测得石雕C在其南偏东30°方向．你认为此方案能够测得该公园的湖心亭A处到南岸的距离吗？若可以，请计算此距离是多少米？（结果保留到小数点后一位）
此方案能够测得该公园的湖心亭A处到南岸的距离．
过点A作南岸所在直线的垂线，垂足是点D．
在Rt△ADC中，
∵∠ADC=90°，∠DAC=45°，
∴DC=AD．
在Rt△BDC中，
∵∠BDC=90°，∠DBC=30°，
∴BD=
CD，
∴BD=
AD．
由题意得：∵BD-AD=AB，
∴
AD-AD=10，
解得AD=13.7．
答：该公园的湖心亭A处到南岸的距离约是13.7米．
过点A作南岸所在直线的垂线，垂足是点D．在Rt△ADC中，
∵∠ADC=90°，∠DAC=45°，
∴DC=AD．
在Rt△BDC中，
∵∠BDC=90°，∠DBC=30°，
∴BD=
| 3 |
∴BD=
| 3 |
由题意得：∵BD-AD=AB，
∴
| 3 |
解得AD=13.7．
答：该公园的湖心亭A处到南岸的距离约是13.7米．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
