题目内容
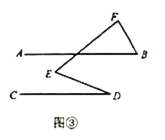
【题目】如图，将矩形ABCD沿BD翻折，点C落在P点处，连接AP．若∠ABP＝26°，则∠APB＝___________
【答案】32°
【解析】分析：根据轴对称的性质和矩形的性质可以得出AB=DP，AP∥BD，进而得出∠APB的度数．
详解：∵△BDC与△BDE关于BD对称，
∴△BDC≌△BDP，
∴BP=BC，DP=DC，∠DBP=∠DBC.
∵四边形ABCD是矩形，
∴AB=CD=DP,AD=BC=BP,AD∥BC，
∴∠ADB=∠CBD，
∴∠PBD=∠ADB，
∴BF=DF，
∴BPBF=ADDF，
∴AF=PF，
∴∠FAP=∠FPA，
∵∠AFP=∠BFD，
∴2∠PAF=2∠ADB，
∴∠PAF=∠ADB，
∴AP∥BD，
∴∠APB=∠PBD，
∵∠ABP=26°，
∴∠CBD=∠DBP=
(90°26°)=32°，
则∠APB=32°.
故答案为：32°.
练习册系列答案
字词句篇与同步作文达标系列答案
走进文言文系列答案
相关题目
