题目内容
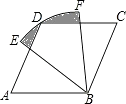
【题目】如图,在△ABC中,AB=AC,D是边BC上一点,DE⊥AB,DF⊥AC,垂足分别是E,F,△AEF∽△ABC.
(1)求证:△AED≌△AFD;
(2)若BC=2AD,求证:四边形AEDF是正方形.
【答案】
(1)证明:∵△AEF∽△ABC,
∴ ![]() =
= ![]() ,
,
∵AB=AC,
∴AE=AF,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
在Rt△AED和Rt△AFD中,
![]() ,
,
∴Rt△AED≌Rt△AFD
(2)证明:∵Rt△AED≌Rt△AFD,
∴∠EAD=∠FAD,
∵AB=AC,
∴AD⊥BC,BC=2BD,
∵BC=2AD,
∴BD=AD,
∵AD⊥BC,
∴∠ADB=90°,
∴∠B=∠BAD=45°,
∴∠BAC=2∠BAD=90°,
∵∠AED=∠AFD=90°,
∴四边形AEDF是矩形,
∵AE=AF,
∴矩形AEDF是正方形
【解析】(1)由相似三角形得性质得AE=AF,然后由HL定理判断出Rt△AED≌Rt△AFD;(2)由Rt△AED≌Rt△AFD得∠EAD=∠FAD,再由等腰三角形的三线合一得AD⊥BC,BC=2BD,由BC=2AD,得出∠B=∠BAD=45°,从而判断四边形AEDF是矩形,最后由一组邻边相等的矩形是正方形得出答案。
【考点精析】通过灵活运用正方形的判定方法和相似三角形的性质,掌握先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角;对应角相等,对应边成比例的两个三角形叫做相似三角形即可以解答此题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目