Question

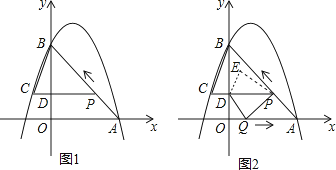
【题目】（探究）如图①，在△ABC中，∠ABC的平分线与∠ACB的平分线相交于点P．

（1）若∠ABC=50°，∠ACB=80°，则∠A=　 　度，∠P=　 　度

（2）∠A与∠P的数量关系为　 　，并说明理由．

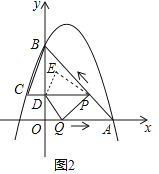
（应用）如图②，在△ABC中，∠ABC的平分线与∠ACB的平分线相交于点P．∠ABC的外角平分线与∠ACB的外角平分线相交于点Q．直接写出∠A与∠Q的数量关系为　 　．

Answer 1

【答案】（1）50，115；（2）（3）

【解析】

根据三角形内角和及角平分线的定义即可算出.

解：（1）∵∠ABC=50°，∠ACB=80°，

∴∠A=50°，

∵∠ABC的平分线与∠ACB的平分线相交于点P，

∴∠CBP=∠ABC，∠BCP=∠ACB，

∴∠BCP+∠CBP=（∠ABC+∠ACB）=×130°=65°，

∴∠P=180°﹣65°=115°，

故答案为：50，115；

（2）．

证明：∵BP、CP分别平分∠ABC、∠ACB，

∴，，

∵∠A+∠ABC+∠ACB=180°∠P+∠PBC+∠PCB=180°，

∴，

∴，

∴；

（3）．

理由：∵∠ABC的外角平分线与∠ACB的外角平分线相交于点Q，

∴∠CBQ=（180°﹣∠ABC）=90°﹣∠ABC，

∠BCQ=（180°﹣∠ACB）=90°﹣∠ACB，

∴△BCQ中，∠Q=180°﹣（∠CBQ+∠BCQ）=180°﹣（90°﹣∠ABC+90°﹣∠ACB）=（∠ABC+∠ACB），

又∵∠ABC+∠ACB=180°﹣∠A，

∴∠Q=（180°﹣∠A）=90°﹣∠A．