题目内容
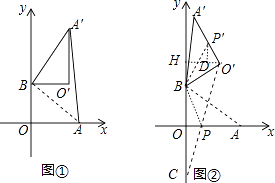
【题目】在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′,记旋转角为α.
(1)如图①,若α=90°,求AA′的长;
(2)如图②,若α=120°,求点O′的坐标;
(3)在(Ⅱ)的条件下,边OA上 的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,求点P′的坐标(直接写出结果即可)
【答案】
(1)
解:如图①,
∵点A(4,0),点B(0,3),
∴OA=4,OB=3,
∴AB= ![]() =5,
=5,
∵△ABO绕点B逆时针旋转90°,得△A′BO′,
∴BA=BA′,∠ABA′=90°,
∴△ABA′为等腰直角三角形,
∴AA′= ![]() BA=5
BA=5 ![]()
(2)
解:作O′H⊥y轴于H,如图②,
∵△ABO绕点B逆时针旋转120°,得△A′BO′,
∴BO=BO′=3,∠OBO′=120°,
∴∠HBO′=60°,
在Rt△BHO′中,∵∠BO′H=90°﹣∠HBO′=30°,
∴BH= ![]() BO′=
BO′= ![]() ,O′H=
,O′H= ![]() BH=
BH= ![]() ,
,
∴OH=OB+BH=3+ ![]() =
= ![]() ,
,
∴O′点的坐标为( ![]() ,
, ![]() )
)
(3)
解:∵△ABO绕点B逆时针旋转120°,得△A′BO′,点P的对应点为P′,
∴BP=BP′,
∴O′P+BP′=O′P+BP,
作B点关于x轴的对称点C,连结O′C交x轴于P点,如图②,
则O′P+BP=O′P+PC=O′C,此时O′P+BP的值最小,
∵点C与点B关于x轴对称,
∴C(0,﹣3),
设直线O′C的解析式为y=kx+b,
把O′( ![]() ,
, ![]() ),C(0,﹣3)代入得
),C(0,﹣3)代入得 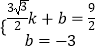 ,解得
,解得 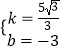 ,
,
∴直线O′C的解析式为y= ![]() x﹣3,
x﹣3,
当y=0时, ![]() x﹣3=0,解得x=
x﹣3=0,解得x= ![]() ,则P(
,则P( ![]() ,0),
,0),
∴OP= ![]() ,
,
∴O′P′=OP= ![]() ,
,
作P′D⊥O′H于D,
∵∠BO′A=∠BOA=90°,∠BO′H=30°,
∴∠DP′O′=30°,
∴O′D= ![]() O′P′=
O′P′= ![]() ,P′D=
,P′D= ![]() O′D=
O′D= ![]() ,
,
∴DH=O′H﹣O′D= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴P′点的坐标为( ![]() ,
, ![]() )
)
【解析】本题考查了几何变换综合题:熟练掌握旋转的性质;理解坐标与图形性质;会利用两点之间线段最短解决最短路径问题;记住含30度的直角三角形三边的关系.(1)如图①,先利用勾股定理计算出AB=5,再根据旋转的性质得BA=BA′,∠ABA′=90°,则可判定△ABA′为等腰直角三角形,然后根据等腰直角三角形的性质求AA′的长;(2)作O′H⊥y轴于H,如图②,利用旋转的性质得BO=BO′=3,∠OBO′=120°,则∠HBO′=60°,再在Rt△BHO′中利用含30度的直角三角形三边的关系可计算出BH和O′H的长,然后利用坐标的表示方法写出O′点的坐标;(3)由旋转的性质得BP=BP′,则O′P+BP′=O′P+BP,作B点关于x轴的对称点C,连结O′C交x轴于P点,如图②,易得O′P+BP=O′C,利用两点之间线段最短可判断此时O′P+BP的值最小,接着利用待定系数法求出直线O′C的解析式为y= ![]() x﹣3,从而得到P(
x﹣3,从而得到P( ![]() ,0),则O′P′=OP=
,0),则O′P′=OP= ![]() ,作P′D⊥O′H于D,然后确定∠DP′O′=30°后利用含30度的直角三角形三边的关系可计算出P′D和DO′的长,从而可得到P′点的坐标.
,作P′D⊥O′H于D,然后确定∠DP′O′=30°后利用含30度的直角三角形三边的关系可计算出P′D和DO′的长,从而可得到P′点的坐标.
【考点精析】本题主要考查了线段的基本性质和含30度角的直角三角形的相关知识点,需要掌握线段公理:所有连接两点的线中,线段最短.也可简单说成:两点之间线段最短;连接两点的线段的长度,叫做这两点的距离;线段的大小关系和它们的长度的大小关系是一致的;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半才能正确解答此题.

【题目】为了解某校学生的身高情况,随机抽取该校若干男生、女生进行抽样调查.已知抽取的样本中,男生、女生人数相同,利用所得数据绘制如下统计表和统计图(如图20-3-2所示):
身高情况分组表(单位:cm)
组别 | 身高 |
A | x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | x≥170 |
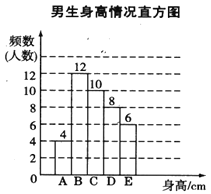
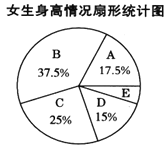
根据图表提供的信息,回答下列问题:
(1)样本中,男生身高的众数在___________组,中位数在___________组;
(2)样本中,女生身高在E组的有___________人;
(3)已知该校共有男生400人、女生380人,请估计身高在160≤x<170范围内的学生约有多少人.