题目内容
已知二次函数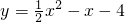 ,
,
(1)求函数图象的顶点坐标,对称轴以及图象与坐标轴的交点;
(2)当x取何值时,y随x的增大而增大?当x取何值时,y随x的增大而减小?
(3)求出函数的最大值或最小值.
解:(1)∵y= x2-x-4
x2-x-4
= (x2-2x+1)-
(x2-2x+1)-
= (x-1)2-
(x-1)2- ,
,
∴顶点坐标为(1,- ),对称轴直线x=1,
),对称轴直线x=1,
令y=0,则 x2-x-4=0,
x2-x-4=0,
整理得,x2-2x-8=0,
解得x1=-2,x2=4,
所以,与x轴的交点坐标是(-2,0),(4,0),
令x=0,则y=-4,
所以,与y轴的交点坐标是(0,-4);
(2)∵a= >0,对称轴为直线x=1,
>0,对称轴为直线x=1,
∴x>1时,y随x的增大而增大,
x<1时,y随x的增大而减小;
(3)∵a= >0,
>0,
∴函数有最小值,为- .
.
分析:(1)把函数解析式转化为顶点式解析式,即可得到顶点坐标与对称轴,令y=0,解方程即可得到与x轴的交点坐标,令x=0求出y的值,即可得到与y轴的交点坐标;
(2)根据二次函数的增减性解答;
(3)根据顶点坐标确定最值即可.
点评:本题考查了抛物线与x轴的交点问题,二次函数的顶点坐标,对称轴,二次函数的增减性,最值问题,其中(1)要注意与坐标轴包括x轴于y轴两种情况,容易漏解而导致出错.
 x2-x-4
x2-x-4=
 (x2-2x+1)-
(x2-2x+1)-
=
 (x-1)2-
(x-1)2- ,
,∴顶点坐标为(1,-
 ),对称轴直线x=1,
),对称轴直线x=1,令y=0,则
 x2-x-4=0,
x2-x-4=0,整理得,x2-2x-8=0,
解得x1=-2,x2=4,
所以,与x轴的交点坐标是(-2,0),(4,0),
令x=0,则y=-4,
所以,与y轴的交点坐标是(0,-4);
(2)∵a=
 >0,对称轴为直线x=1,
>0,对称轴为直线x=1,∴x>1时,y随x的增大而增大,
x<1时,y随x的增大而减小;
(3)∵a=
 >0,
>0,∴函数有最小值,为-
 .
.分析:(1)把函数解析式转化为顶点式解析式,即可得到顶点坐标与对称轴,令y=0,解方程即可得到与x轴的交点坐标,令x=0求出y的值,即可得到与y轴的交点坐标;
(2)根据二次函数的增减性解答;
(3)根据顶点坐标确定最值即可.
点评:本题考查了抛物线与x轴的交点问题,二次函数的顶点坐标,对称轴,二次函数的增减性,最值问题,其中(1)要注意与坐标轴包括x轴于y轴两种情况,容易漏解而导致出错.

练习册系列答案
相关题目
已知二次函数y=-x2+bx+c的图象过点A(1,2),B(3,2),C(0,-1),D(2,3).点P(x1,y1),Q(x2,y2)也在该函数的图象上,当0<x1<1,2<x2<3时,y1与y2的大小关系正确的是( )
| A、y1≥y2 | B、y1>y2 | C、y1<y2 | D、y1≤y2 |
 (2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
(2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;