题目内容
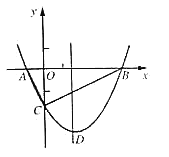
【题目】扫地机器人能够自主移动并作出反应,是因为它发射红外信号反射回接收器,机器人在打扫房间时,若碰到障碍物则发起警报.若某一房间内A、B两点之间有障碍物,现将A、B两点放置于平面直角坐标系xOy中(如图),已知点A,B的坐标分别为(0,4),(6,4),机器人沿抛物线y=ax2﹣4ax﹣5a运动.若机器人在运动过程中只触发一次报警,则a的取值范围是_____.

【答案】﹣![]() <a<
<a<![]()
【解析】
根据题意可以知道抛物线与线段AB有一个交点,根据抛物线对称轴及其与y轴的交点即可求解.
解:由题意可知:
∵点A、B坐标分别为(0,4),(6,4),
∴线段AB的解析式为y=4.
机器人沿抛物线y=ax2﹣4ax﹣5a运动.
抛物线对称轴方程为:x=2,
机器人在运动过程中只触发一次报警,
所以抛物线与线段y=4只有一个交点.
所以抛物线经过点A下方.
∴﹣5a<4
解得a>﹣![]() .
.
4=ax2﹣4ax﹣5a,
△=0
即36a2+16a=0,
解得a1=0(不符合题意,舍去),a2=![]() .
.
当抛物线恰好经过点B时,
即当x=6,y=4时,
36a﹣24a﹣5a=4,
解得a=![]()
综上:a的取值范围是﹣![]() <a<
<a<![]()

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目