题目内容
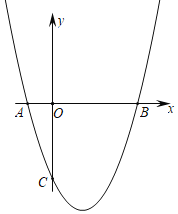
【题目】在平面直角坐标系中有![]() ,
,![]() 为原点,
为原点,![]() ,
,![]() ,将此三角形绕点
,将此三角形绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,抛物线
,抛物线![]()
![]() 过
过![]() 三点.
三点.
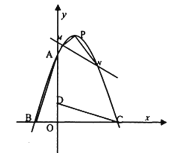
(1)求此抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)直线![]() 与抛物线交于
与抛物线交于![]() 两点,若
两点,若![]() ,求
,求![]() 的值;
的值;
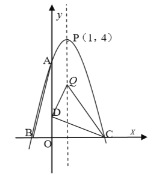
(3)抛物线的对称轴上是否存在一点![]() 使得
使得![]() 为直角三角形.
为直角三角形.
【答案】(1)![]() ;点
;点![]() ;(2)
;(2)![]() ;(3)存在,Q1(1,-1),Q2(1,2), Q3(1,4), Q4(1,-5).
;(3)存在,Q1(1,-1),Q2(1,2), Q3(1,4), Q4(1,-5).
【解析】
(1)用待定系数法可求抛物线的解析式,进行配成顶点式即可写出顶点坐标;
(2)将直线与抛物线联立,通过根与系数关系得到![]() ,
,![]() ,再通过
,再通过![]() 得出
得出![]() ,通过变形得出
,通过变形得出![]() 代入即可求出
代入即可求出![]() 的值;
的值;
(3)分:![]() ,
, ![]() ,
, ![]() 三种情况分别利用勾股定理进行讨论即可.
三种情况分别利用勾股定理进行讨论即可.
(1)∵![]() ,
,![]() ,
,
![]()
∵![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,
,
![]()
∴点![]() 的坐标为:
的坐标为:![]() ,
,
将点A,B代入抛物线![]() 中得
中得
![]() 解得
解得![]()
∴此抛物线的解析式为:![]()
∵![]() ;
;
∴点![]()
(2)直线![]() :
:![]() 与抛物线的对称轴交点
与抛物线的对称轴交点![]() 的坐标为
的坐标为![]() ,
,
交抛物线于![]() ,
,![]() ,
,![]()
由![]() 得:
得:![]()
∴![]() ,
,![]()
∵![]() ,
,
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()

(3)存在,![]() 或
或![]() ,
,![]() ,
,![]()
![]()
∴![]()
设点![]()
![]() ,
,![]()
若![]() ,则
,则![]()
即![]()
∴![]() 或
或![]()
若![]() ,则
,则![]()
即![]()
∴![]()
若![]() ,则
,则![]()
即![]()
∴![]()
即Q1(1,-1), Q2(1,2), Q3(1,4), Q4(1,-5).

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目