题目内容
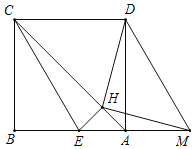
【题目】如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到.若过点E作EH⊥AC,H为垂足,则有以下结论:①点M位置变化,使得∠DHC=60°时,2BE=DM;②无论点M运动到何处,都有DM=![]() HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.
HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.
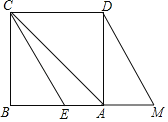
【答案】①②③
【解析】先判定△MEH≌△DAH(SAS),即可得到△DHM是等腰直角三角形,进而得出DM=![]() HM;依据当∠DHC=60°时,∠ADH=60°﹣45°=15°,即可得到Rt△ADM中,DM=2AM,即可得到DM=2BE;依据点M是边BA延长线上的动点(不与点A重合),且AM<AB,可得∠AHM<∠BAC=45°,即可得出∠CHM>135°.
HM;依据当∠DHC=60°时,∠ADH=60°﹣45°=15°,即可得到Rt△ADM中,DM=2AM,即可得到DM=2BE;依据点M是边BA延长线上的动点(不与点A重合),且AM<AB,可得∠AHM<∠BAC=45°,即可得出∠CHM>135°.
由题可得,AM=BE,
∴AB=EM=AD,
∵四边形ABCD是正方形,EH⊥AC,
∴EM=AH,∠AHE=90°,∠MEH=∠DAH=45°=∠EAH,
∴EH=AH,
∴△MEH≌△DAH(SAS),
∴∠MHE=∠DHA,MH=DH,
∴∠MHD=∠AHE=90°,△DHM是等腰直角三角形,
∴DM=![]() HM,故②正确;
HM,故②正确;
当∠DHC=60°时,∠ADH=60°﹣45°=15°,
∴∠ADM=45°﹣15°=30°,
∴Rt△ADM中,DM=2AM,
即DM=2BE,故①正确;
∵点M是边BA延长线上的动点(不与点A重合),且AM<AB,
∴∠AHM<∠BAC=45°,
∴∠CHM>135°,故③正确,
故答案为:①②③.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案【题目】抛物线![]() 上部分点坐标如表所示,下列说法错误的是( )
上部分点坐标如表所示,下列说法错误的是( )
x | … | -3 | -2 | -1 | 0 | 1 | … |
y | … | -6 | 0 | 4 | 6 | 6 | … |
A. 抛物线与y轴的交点为(0,6) B. 抛物线的对称轴是在y轴的右侧;
C. 抛物线一定经过点(3,0) D. 在对称轴左侧,y随x增大而减小.