题目内容
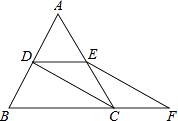
【题目】如图，等边△ABC的边长是2，D、E分别为AB、AC的中点，延长BC至点F，使CF= 
BC，连接CD和EF． 
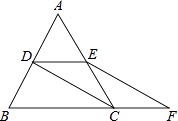
（1）求证：DE=CF；
（2）求EF的长．
【答案】
（1）证明：∵D、E分别为AB、AC的中点，
∴DE 
BC，
∵延长BC至点F，使CF= BC，
∴DE FC，
即DE=CF
（2）解：∵DE FC，
∴四边形DEFC是平行四边形，
∴DC=EF，
∵D为AB的中点，等边△ABC的边长是2，
∴AD=BD=1，CD⊥AB，BC=2，
∴DC=EF= 
．
【解析】（1）直接利用三角形中位线定理得出DE BC，进而得出DE=FC；（2）利用平行四边形的判定与性质得出DC=EF，进而利用等边三角形的性质以及勾股定理得出EF的长．
【考点精析】利用等边三角形的性质和三角形中位线定理对题目进行判断即可得到答案，需要熟知等边三角形的三个角都相等并且每个角都是60°；连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半．
【题目】为了贯彻落实市委政府提出的“精准扶贫”精神，某校特制定了一系列帮扶A、B两贫困村的计划，现决定从某地运送152箱鱼苗到A、B两村养殖，若用大小货车共15辆，则恰好能一次性运完这批鱼苗，已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆，其运往A、B两村的运费如表：
目的地 | A村（元/辆） | B村（元/辆） |
大货车 | 800 | 900 |
小货车 | 400 | 600 |
（1）求这15辆车中大小货车各多少辆？
（2）现安排其中10辆货车前往A村，其余货车前往B村，设前往A村的大货车为x辆，前往A、B两村总费用为y元，试求出y与x的函数解析式．
（3）在（2）的条件下，若运往A村的鱼苗不少于100箱，请你写出使总费用最少的货车调配方案，并求出最少费用．
【题目】八（2）班组织了一次经典朗读比赛，甲、乙两队各10人的比赛成绩如下表（10分制）：
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
（1）甲队成绩的中位数是分，乙队成绩的众数是分；
（2）计算乙队的平均成绩和方差；
（3）已知甲队成绩的方差是1.4分2 ， 则成绩较为整齐的是队．
