题目内容
在平行四边形ABCD中,E、F分别为对角线BD上的两点,且BE=DF.
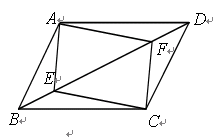
(1)试说明四边形AECF是平行四边形;
(2)连结AC,当EF与AC满足 时,四边形AECF是菱形,依据是 (不必证明)
(3)连结AC,当EF与AC满足 时,四边形AECF是矩形.依据是 (不必证明)

(1)试说明四边形AECF是平行四边形;
(2)连结AC,当EF与AC满足 时,四边形AECF是菱形,依据是 (不必证明)
(3)连结AC,当EF与AC满足 时,四边形AECF是矩形.依据是 (不必证明)
见解析
试题分析:解:(1)
连接AC交BD于O
∵四边形ABCD是平行四边形
∴AO=CO BO=DO
又∵BE=DF
∴EO=FO
∴四边形AECF是平行四边形
(对角线互相平分的四边形是平行四边形)
(答案不唯一)
(2)AC⊥EF
对角线互相垂直的平行四边形是菱形
(3)AC = EF
对角线相等的平行四边形是矩形
点评: 此类试题属于难度较大的试题,考生解答此类试题时一定要把握好平行四边形的基本性质定理和判定定理,菱形的性质定理和判定定理,矩形的性质定理和判定定理。

练习册系列答案
相关题目
 的一条对角线
的一条对角线 平移
平移 的位置,
的位置, 是等腰三角形吗?为什么?(6分)
是等腰三角形吗?为什么?(6分)
 、
、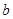 、
、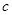 、
、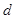 ,且
,且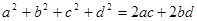 ,则这个四边形为 ;
,则这个四边形为 ;