题目内容

在直角坐标系中，已知两点A、B以及动点C、D，则当以点A、 B、C 、D为顶点的四边形的周长最小时，比值为     ．

试题分析：先根据两点间的距离公式求出AB的值，再过点B作关于y轴的对称点B′，过点A作关于x轴的对称点A′，连接A′B′分别交x、y轴于点D、C，由两点之间线段最短可知线段A′B′即为四边形ABCD的周长最小值，用待定系数法求出过A′B′两点的直线解析式，即可求出C、D的坐标．

∴四边形ABCD周长=AB+BC+CD+AD=2+BC+CD+AD，
∴求其周长最小值，就是求BC+CD+AD的最小值．过B作y轴对称点B′（4，5），
则BC=B′C，
过A作x轴对称点A′（-8，-3），则AD=A′D
  
∴BC+CD+AD=B′C+CD+A′D≥A′B′
即A′、D、C、B′四点共线时取等号
可求出相应的C、D坐标，
设直线A′B′的方程是y=kx+b（k≠0），


点评：根据对称的性质作出A、B的对称点A′、B′及求出其坐标是解答此题的关键．
练习册系列答案
相关题目
如果点P(在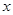轴上，则点P的坐标为（    ）
A．(0，2)B．(2，0) C．(4，0)D．(0，
若线段AB的端点A的坐标为（﹣2，﹣3），现将线段AB沿y轴向下平移2个单位，则点A经过平移后的对应点A′的坐标是（　　）
A．（﹣2，﹣1）B．（﹣2，﹣5）C．（0，﹣3）D．（﹣4，﹣3）
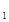定义：平面内的两条直线l与l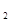相交于点O，对于该平面内任意一点M，M点到直线l，l的距离分别为a、b，则称有序非负实数对（a，b）是点M的“距离坐标”．根据上述定义，“距离坐标”为（2，3）的点的个数是
A．1B．2 C．3D．4
如图所示的正方形网格中，确定格点D的位置，使得以A、B、C、D为顶点的四边形为等腰梯形，则点D的位置应在（    ）

A、点M处             B、点N处         C、点P处        D、点Q处
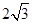如图,已知点A（0,2）、B（ ,2）、C(0,4),过点C向右作平行于x轴的射线,点P是射线上的动点,连结AP,以AP为边在其左侧作等边△APQ ,连结PB、BA.若四边形ABPQ为梯形,则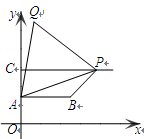

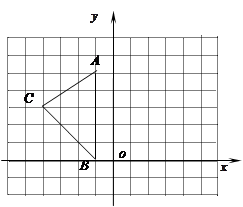
（1）当AB为梯形的底时,点P的横坐标是     ；
（2）当AB为梯形的腰时,点P的横坐标是     .
如图：在平面直角坐标系中A( - 1, 5 ),　B( - 1, 0 )　C( - 4, 3 ).

（1）在图中作出△ABC关于y轴对称图形△A1B1C1, 直接在图中写出C1的坐标(２分)
（2）在x轴上找一点P, 使得PA＋PC1的值最小，并求出P点坐标。（5分）
线段CD是由线段AB平移得到的，点A（-1，4）的对应点为C（4，7），则点B（-4，-1）的对应点的坐标为（ ）
A．（2，9）B．（5，3）C．（1，2）D．（-9，-4）
如图所示的象棋盘上，若“帅”位于点上，“相”位于点上，则“炮”位于点   .

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网