题目内容
如图:在平面直角坐标系中A( - 1, 5 ), B( - 1, 0 ) C( - 4, 3 ).
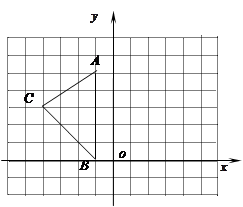
(1)在图中作出△ABC关于y轴对称图形△A1B1C1, 直接在图中写出C1的坐标(2分)
(2)在x轴上找一点P, 使得PA+PC1的值最小,并求出P点坐标。(5分)
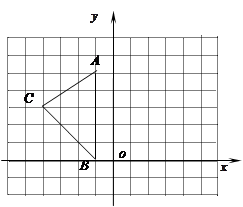
(1)在图中作出△ABC关于y轴对称图形△A1B1C1, 直接在图中写出C1的坐标(2分)
(2)在x轴上找一点P, 使得PA+PC1的值最小,并求出P点坐标。(5分)
(1)

(2)P的坐标为(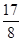 ,0)
,0)

(2)P的坐标为(
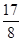 ,0)
,0)试题分析:(1)利用轴对称性质,作出A、B、C关于y轴的对称点,A1、B1、C1,顺次连接A1B1、B1C1、C1A1,即得到关于y轴对称的△A1B1C1;如图

(2)作点C1关于x轴的对称点D(4,-3),
连接AD交x轴于P点,此时PA+PC1的
值最小,设直线AD的关系式为y=kx+b,
则
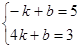 解得
解得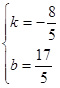
所以直线AD的关系式为
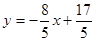
当y = 0时,
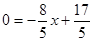 解得
解得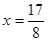 ,所以P的坐标为(
,所以P的坐标为(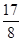 ,0)
,0)点评:本题考查轴对称图形、直线,解答本题时要求考生掌握轴对称图形的概念,会做一个图形的轴对称图形、会求两直线的交点坐标

练习册系列答案
相关题目
 、B
、B 以及动点C
以及动点C 、D
、D ,则当以点A、 B、C 、D为顶点的四边形的周长最小时,比值
,则当以点A、 B、C 、D为顶点的四边形的周长最小时,比值 为 .
为 . ,将线段AB经过平移后得到线段
,将线段AB经过平移后得到线段 ,若点A的对应点为
,若点A的对应点为 ,则点B的对应点
,则点B的对应点 的坐标是 .
的坐标是 .
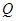 关于
关于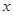 轴对称,则
轴对称,则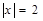 ,
,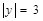 则点P的坐标为( )
则点P的坐标为( )