题目内容
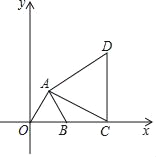
【题目】在平面直角坐标系中，△AOB为等边三角形，B（2，0），直线l：y=kx+b经过点B，点C是x轴正半轴上的一动点，以线段AC为边在第一象限作等边△ACD．
（1）直接写出点A的坐标：A（ ， ），当直线l经过点A时，求直线BA的表达式．
（2）当直线l经过点D时，直线与y轴相交于点F，随着点C的变化，点F的位置是否发生变化？若没有变化，求出此时点F的坐标．；若有变化，请说明理由．
（3）当直线与线段OA相交与点E时，如果直线l把△AOB的面积分为1：2两部分，求出此时点E的坐标．
（4）若点C的坐标为（4，0）时，直线l与线段AD有交点，请直接写出此时k的取值范围．
【答案】（1）A（1，
）;（2）点F的位置不会发生变化，为F（0，-2）;(3) E（
，
），E′（
，
）；（4）x≤
或者x≥
【解析】
（1）如图，作AH⊥OB于H，解直角三角形求出AH即可，利用待定系数法求出直线AB的解析式即可；
（2）由△OAC≌△BAD（SAS），推出BD∥OA，求出直线BD的解析式即可解决问题；
（3）分两种情况分别求解即可解决问题；
（4）求出直线AB，BD的解析式即可判断k的取值范围.
解：（1）如图，作AH⊥OB于H．
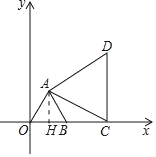
∵B（2，0），△ABC是等边三角形，
∴OA=OB=AB=2，
∵AH⊥OB，
∴OH=HB=1，
∴AH=
=
∴A（1，），
把A，B坐标代入y=kx+b得到：
，
解之得
，
所以直线AB解析式为
．
故答案为1，
．
（2）作直线BD，由已知AO=AB，AC=AO，
又∠OAB=∠CAD，
∠OAB+∠BAC=∠CAD+∠BAC
∠OAC=∠BAD
△OAC≌△BAD（SAS）
∠AOC=∠ABD=60°，
∵∠OAB=∠AOB=60°，
∴∠OAB=∠ABD=60°，
∴BD∥OA
∵直线OA的解析式为
，
设直线BD：
，则
，
所以b1=
，
即点F的位置不会发生变化，为F（0，
）．
（3）有两种情况，
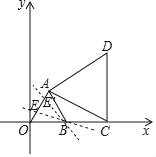
当OE=
OA或OE′=
OA时，满足条件，
∵A（1，
），
∴E（， ），E′（ ，）；
（4）如图，
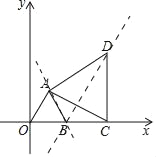
当C（4，0）时，易知：AB=BC=2，
∴∠BAC=∠BCA，
∵∠ABO=60°=∠BAC+∠BCA，
∴∠BCA=∠BAC=30°，
∵∠ACD=∠OAB=60°，
∴∠DCB=∠OAC=90°，
∴AC=OA=2，
∴D（4，2），
∵直线AB的解析式为y=﹣+2
，
当直线l经过点D时，直线l的解析式为y=x﹣2，
观察图象可知满足条件的k的值为x≤
或者x≥．
