Question

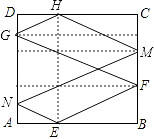
【题目】如图，正方形ABCD的边长为3，点E，F分别在边AB，BC上，AE=BF=1，小球P从点E出发沿直线向点F运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角．当小球P第一次碰到点E时，小球P与正方形的边碰撞的次数为 ， 小球P所经过的路程为 ．

Answer 1

【答案】6；6
【解析】解：根据已知中的点E，F的位置，可知入射角的正切值为 ，第一次碰撞点为F，在反射的过程中，根据入射角等于反射角及平行关系的三角形的相似可得， 第二次碰撞点为G，在DA上，且DG= DA，
第三次碰撞点为H，在DC上，且DH= DC，
第四次碰撞点为M，在CB上，且CM= BC，
第五次碰撞点为N，在DA上，且AN= AD，
第六次回到E点，AE= AB．
由勾股定理可以得出EF= ，FG= ，GH= ，HM= ，MN= ，NE= ，
故小球经过的路程为： + + + + + =6 ，
所以答案是：6；6 ．

【考点精析】通过灵活运用正方形的性质和轴对称的性质，掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形；关于某条直线对称的两个图形是全等形；如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线；两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上即可以解答此题．