题目内容
阅读材料:
在平面直角坐标系中,已知x轴上两点A(x1,0),B(x2,0)的距离记作|AB|=|x1-x2|,如果A(x1,y1),B(x2,y2)是平面上任意两点,我们可以通过构造直角三角形来求AB间距离.
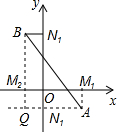
如图,过A,B分别向x轴,y轴作垂线AM1、AN1和BM2、BN2,垂足分别是M1(x1,0),N1(0,y1),M2(x2,0),N2(0,y2),直线AN1交BM2于Q点,在Rt△ABQ中,|AB|2=|AQ|2+|QB|2.
∵|AQ|=|M1M2|=|x2-x1|,|QB|=|N1N2|=|y2-y1|,∴|AB|2=|x2-x1|2+|y2-y1|2.
由此得任意两点[A(x1,y1),B(x2,y2)]间距离公式为:|AB|=
.
(1)直接应用平面内两点间距离公式计算,点A(1,-3),B(-2,1)之间的距离为______;
(2)平面直角坐标系中的两点A(1,3)、B(4,1),P为x轴上任一点,当PA+PB最小时,直接写出点P的坐标为______,PA+PB的最小值为______;
(3)应用平面内两点间距离公式,求代数式
+
的最小值.
在平面直角坐标系中,已知x轴上两点A(x1,0),B(x2,0)的距离记作|AB|=|x1-x2|,如果A(x1,y1),B(x2,y2)是平面上任意两点,我们可以通过构造直角三角形来求AB间距离.
如图,过A,B分别向x轴,y轴作垂线AM1、AN1和BM2、BN2,垂足分别是M1(x1,0),N1(0,y1),M2(x2,0),N2(0,y2),直线AN1交BM2于Q点,在Rt△ABQ中,|AB|2=|AQ|2+|QB|2.
∵|AQ|=|M1M2|=|x2-x1|,|QB|=|N1N2|=|y2-y1|,∴|AB|2=|x2-x1|2+|y2-y1|2.
由此得任意两点[A(x1,y1),B(x2,y2)]间距离公式为:|AB|=
| (x2-x1)2+(y2-y1)2 |
(1)直接应用平面内两点间距离公式计算,点A(1,-3),B(-2,1)之间的距离为______;
(2)平面直角坐标系中的两点A(1,3)、B(4,1),P为x轴上任一点,当PA+PB最小时,直接写出点P的坐标为______,PA+PB的最小值为______;
(3)应用平面内两点间距离公式,求代数式
| x2+(y-2)2 |
| (x-3)2+(y-1)2 |

(1)|AB|=
=5;
故答案为:5;
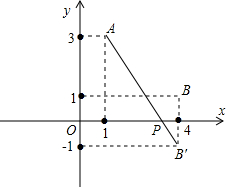
(2)如图,作点B关于x轴对称的点B′,连接AB′,直线AB′于x轴的交点即为所求的点P.
①∵B(4,1),
∴B′(4,-1).
又∵A(1,3),
∴直线AB的解析式为:y=-
x+
,
当y=0时,x=
,即P(
,0);
②PA+PB=PA+PB′=AB′=
=5,即
PA+PB的最小值为.
故答案为:(
,0);5;
(3)
+
=
+
故原式表示点(x,y)到点(0,2)和(3,1)的距离之和,
由两点之间线段最短可得:点(x,y)在以(0,2)和(3,1)为端点的线段上时,代数式
+
取最小值.
原式最小为
=
.
| (-2-1)2+(1+3)2 |
故答案为:5;
(2)如图,作点B关于x轴对称的点B′,连接AB′,直线AB′于x轴的交点即为所求的点P.
①∵B(4,1),
∴B′(4,-1).
又∵A(1,3),
∴直线AB的解析式为:y=-
| 4 |
| 3 |
| 13 |
| 3 |
当y=0时,x=
| 13 |
| 4 |
| 13 |
| 4 |
②PA+PB=PA+PB′=AB′=
| (4-1)2+(-1-3)2 |
PA+PB的最小值为.
故答案为:(
| 13 |
| 4 |
(3)
| x2+(y-2)2 |
| (x-3)2+(y-1)2 |
| (x-0)2+(y-2)2 |
| (x-3)2+(y-1)2 |
故原式表示点(x,y)到点(0,2)和(3,1)的距离之和,
由两点之间线段最短可得:点(x,y)在以(0,2)和(3,1)为端点的线段上时,代数式
| x2+(y-2)2 |
| (x-3)2+(y-1)2 |
原式最小为
| (0-3)2+(2-1)2 |
| 10 |


练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目


 x(时)的关系如图所示,根据图象回答:
x(时)的关系如图所示,根据图象回答: