题目内容
【题目】阅读下面材料:
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为∣AB∣.
当A、B两点中有一点在原点时,不妨设点A在原点,如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;
![]()
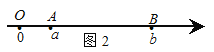
当A、B两点都不在原点时,如图2,点A、B都在原点的右边
∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=![]() =∣a-b∣;
=∣a-b∣;
如图3,当点A、B都在原点的左边,
∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=![]() =∣a-b∣;
=∣a-b∣;
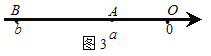
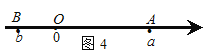
如图4,当点A、B在原点的两边,
∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣= ![]() =∣a-b∣;
=∣a-b∣;
回答下列问题:
(1)数轴上表示1和6的两点之间的距离是 ,数轴上表示2和-3的两点之间的距离是 ;
(2)数轴上若点A表示的数是x,点B表示的数是-4,则点A和B之间的距离是 ,若∣AB∣=3,那么x为 ;
(3)当x是 时,代数式![]() ;
;
(4)若点A表示的数![]() ,点B与点A的距离是10,且点B在点A的右侧,动点P、Q同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒
,点B与点A的距离是10,且点B在点A的右侧,动点P、Q同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒![]() 个单位长度,求运动几秒后,点Q与点P 相距1个单位?(请写出必要的求解过程)
个单位长度,求运动几秒后,点Q与点P 相距1个单位?(请写出必要的求解过程)
【答案】(1)5 ;5(2)![]() ;-7或-1(3)-4或3(4)
;-7或-1(3)-4或3(4)![]() ;
;![]()
【解析】试题分析:
(1)由阅读材料内容可知:若数轴上任意两点A、B所表示的数分别为:a、b,则A、B两点间的距离![]() ,由此可计算本题答案;
,由此可计算本题答案;
(2)同(1)可解得第一空的答案;根据(1)中的公式和绝对值的意义,可列方程解得第二空的答案;
(3)由阅读材料可知:![]() 表示在数轴上表示数“x”的点到表示数“-2”和数“1”这两个点的距离之和等于7,我们分
表示在数轴上表示数“x”的点到表示数“-2”和数“1”这两个点的距离之和等于7,我们分![]() 、
、![]() 和
和![]() 三种情况来化简式子
三种情况来化简式子![]() 就可求得“x”的值;
就可求得“x”的值;
(4)由题意可知:点A表示的数为“-1”,点B表示的数是“9”,则由已知可得:![]() ,
,![]() ,当P与Q相距1个单位长度时,要分点Q在点P右边和点Q在点P左边两种情况来讨论,如图1和图2,列出方程可求解;
,当P与Q相距1个单位长度时,要分点Q在点P右边和点Q在点P左边两种情况来讨论,如图1和图2,列出方程可求解;
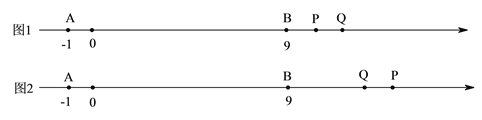
试题解析:
(1)∵![]() ,
,
∴两空都应填“5”;
(2)∵数轴上若点A表示的数是x,点B表示的数是-4,
∴![]() ;
;
又∵![]() ,
,
∴![]() ,即
,即![]() ,解得:
,解得:![]() 或
或![]() ;
;
(3)由阅读材料可知:![]() 表示在数轴上表示数“x”的点到表示数“-2”和数“1”这两个点的距离之和等于7,所以要我们分
表示在数轴上表示数“x”的点到表示数“-2”和数“1”这两个点的距离之和等于7,所以要我们分![]() 、
、![]() 和
和![]() 三种情况来讨论:
三种情况来讨论:
①当![]() 时,
时,![]() 可化为:
可化为:![]() ,解得:
,解得:![]() ;
;
②当![]() 时,
时,![]() 可化为:
可化为:![]() ,该式子不成立;
,该式子不成立;
③当![]() 时,
时,![]() 可化为:
可化为:![]() ,解得;
,解得;![]() ;
;
综上所述:![]() 或
或![]() ;
;
(4)由题意可知:点A表示的数为“-1”,点B表示的数是“9”,则由已知可得:
![]() ,
,![]() ,当P与Q相距1个单位长度时,要分点Q在点P右边和点Q在点P左边两种情况来讨论:
,当P与Q相距1个单位长度时,要分点Q在点P右边和点Q在点P左边两种情况来讨论:
①如图1,当Q在P的右边时,由![]() 可得:
可得:![]() ,即
,即![]() ,解得:
,解得:![]() ;
;
②如图2,当Q在P的左边时,由![]() 可得:
可得:![]() ,即
,即![]() ,解得
,解得![]() ;
;
综上所述:![]() 或
或![]() .
.

 智慧小复习系列答案
智慧小复习系列答案