题目内容
(1)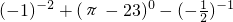 .
.
(2)先化简再求值:(m+1)2-5(m+1)(m-1)+3(m-1)2,其中m=- .
.
解:(1)原式=1+1+2=4;
(2)原式=m2+1+2m-5m2+5+3m2-6m+3
=-m2-4m+9.
当m=- 时,
时,
原式=-m2-4m+9
=-(- )2+4×
)2+4× +9
+9
=11 .
.
分析:(1)先算负整数指数幂和零指数幂,再合并同类项;
(2)运用平方差公式和完全平方公式计算,再合并同类项,然后将m的值代入计算.
点评:(1)第一题主要考查了负整数指数幂和零指数幂的运算;
(2)第二题主要考查了平方差公式、完全平方公式和合并同类项及代入求值的方法.
(2)原式=m2+1+2m-5m2+5+3m2-6m+3
=-m2-4m+9.
当m=-
 时,
时,原式=-m2-4m+9
=-(-
 )2+4×
)2+4× +9
+9=11
 .
.分析:(1)先算负整数指数幂和零指数幂,再合并同类项;
(2)运用平方差公式和完全平方公式计算,再合并同类项,然后将m的值代入计算.
点评:(1)第一题主要考查了负整数指数幂和零指数幂的运算;
(2)第二题主要考查了平方差公式、完全平方公式和合并同类项及代入求值的方法.

练习册系列答案
相关题目