题目内容
已知抛物线![]() 的顶点为(1,0),且经过点(0,1).
的顶点为(1,0),且经过点(0,1).
(1)求该抛物线对应的函数的解析式;
(2)将该抛物线向下平移![]() 个单位,设得到的抛物线的顶点为A,与
个单位,设得到的抛物线的顶点为A,与![]() 轴的两个交点为B、C,若△ABC为等边三角形.
轴的两个交点为B、C,若△ABC为等边三角形.
①求![]() 的值;
的值;
②设点A关于![]() 轴的对称点为点D,在抛物线上是否存在点P,使四边形CBDP为菱形?若存在,写出点P的坐标;若不存在,请说明理由.
轴的对称点为点D,在抛物线上是否存在点P,使四边形CBDP为菱形?若存在,写出点P的坐标;若不存在,请说明理由.
解:(1)由题意可得,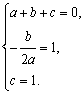 解得
解得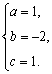
∴抛物线对应的函数的解析式为![]() .………………………………3分
.………………………………3分
(2)①将![]() 向下平移
向下平移![]() 个单位得:
个单位得:![]() -
-![]() =
=![]() ,可知A(1,-
,可知A(1,-![]() ),B(1-
),B(1-![]() ,0),C(1+
,0),C(1+![]() ,0),BC=2
,0),BC=2![]() .……………………………6分
.……………………………6分
由△ABC为等边三角形,得![]() ,由
,由![]() >0,解得
>0,解得![]() =3.…………7分
=3.…………7分
②不存在这样的点P. ……………………………………………………………8分
∵点D与点A关于![]() 轴对称,∴D(1,3).由①得BC=2
轴对称,∴D(1,3).由①得BC=2![]() .要使四边形CBDP为菱形,需DP∥BC,DP=BC.
.要使四边形CBDP为菱形,需DP∥BC,DP=BC.
由题意,知点P的横坐标为1+2![]() ,
,
当![]() =1+2
=1+2![]() 时
时![]() -m=
-m=![]() =
=![]() ,故不存在这样的点P.……………………………………………………………………11分
,故不存在这样的点P.……………………………………………………………………11分
【相关知识点】确定二次函数的表达式;二次函数的性质;关于轴的对称点的性质;等边三角形的性质;菱形的判定
【解题思路】二次函数的图象与性质是中考的重点与难点,因而应高度重视,本题属于综合性较强的题目,应理清思路,对每一个知识点都应熟练掌握并能灵活运用,本题求出二次函数的解析式是解此题的关键,应熟练掌握三点式和顶点式求抛物线解析式的方法;二次函数的平移通常指的是图象的平移,应注意总结平移的规律.

练习册系列答案
相关题目
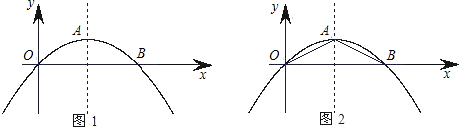
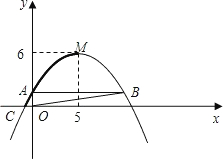 物线图象的一部分,如图中的粗线所示)在平移过程中所扫过的面积.
物线图象的一部分,如图中的粗线所示)在平移过程中所扫过的面积.
 (2012•衡阳)如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)
(2012•衡阳)如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)