题目内容
如图1,已知抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B.(1)求抛物线的解析式;
(2)若点C在抛物线的对称轴上,点D在抛物线上,且以O、C、D、B四点为顶点的四边形为平行四边形,求D点的坐标;
(3)连接OA、AB,如图2,在x轴下方的抛物线上是否存在点P,使得△OBP与△OAB相似?若存在,求出P点的坐标;若不存在,说明理由.
分析:(1)已知抛物线的顶点为A(2,1),设抛物线顶点式,把点O(0,0)代入即可求解析式;
(2)依题意得CD∥OB,CD=OB=4,又对称轴x=2,故D点横坐标x=6,代入抛物线解析式可求D点纵坐标,根据对称轴可求满足条件的点D′;
(3)根据抛物线对称轴可知AO=AB,△AOB为等腰三角形,要使得△OBP与△OAB相似,则∠POB=∠BOA,A与A′对称,可求直线OP的解析式,与抛物线解析式联立可求P点坐标,检验BP与OB是否相等.
(2)依题意得CD∥OB,CD=OB=4,又对称轴x=2,故D点横坐标x=6,代入抛物线解析式可求D点纵坐标,根据对称轴可求满足条件的点D′;
(3)根据抛物线对称轴可知AO=AB,△AOB为等腰三角形,要使得△OBP与△OAB相似,则∠POB=∠BOA,A与A′对称,可求直线OP的解析式,与抛物线解析式联立可求P点坐标,检验BP与OB是否相等.
解答:解:(1)由题意可设抛物线的解析式为
y=a(x-2)2+1
∵抛物线过原点,
∴0=a(0-2)2+1,
∴a=-
.
抛物线的解析式为y=-
(x-2)2+1,
即y=-
x2+x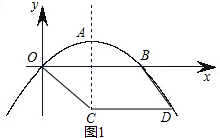
(2)如图1,当四边形OCDB是平行四边形时,CD=OB,
由0=-
(x-2)2+1得x1=0,x2=4,
∴B(4,0),OB=4.
由于对称轴x=2
∴D点的横坐标为6.
将x=6代入y=-
(x-2)2+1,得y=-3,
∴D(6,-3);
根据抛物线的对称性可知,
在对称轴的左侧抛物线上存在点D,使得四边形ODCB是平行四边形,此时D点的坐标为(-2,-3),
当四边形OCBD是平行四边形时,D点即为A点,此时D点的坐标为(2,1)
(3)不存在.
如图2,由抛物线的对称性可知:AO=AB,∠AOB=∠ABO.
若△BOP与△AOB相似,必须有∠POB=∠BOA=∠BPO
设OP交抛物线的对称轴于A′点,显然A′(2,-1)
∴直线OP的解析式为y=-
x
由-
x=-
x2+x,得x1=0,x2=6.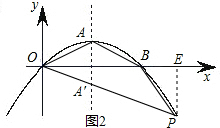
∴P(6,-3)
过P作PE⊥x轴,在Rt△BEP中,BE=2,PE=3,
∴PB=
≠4.
∴PB≠OB,
∴∠BOP≠∠BPO,
∴△PBO与△BAO不相似,
同理可说明在对称轴左边的抛物线上也不存在符合条件的P点.
所以在该抛物线上不存在点P,使得△BOP与△AOB相似.
y=a(x-2)2+1
∵抛物线过原点,
∴0=a(0-2)2+1,
∴a=-
| 1 |
| 4 |
抛物线的解析式为y=-
| 1 |
| 4 |
即y=-
| 1 |
| 4 |

(2)如图1,当四边形OCDB是平行四边形时,CD=OB,
由0=-
| 1 |
| 4 |
∴B(4,0),OB=4.
由于对称轴x=2
∴D点的横坐标为6.
将x=6代入y=-
| 1 |
| 4 |
∴D(6,-3);
根据抛物线的对称性可知,
在对称轴的左侧抛物线上存在点D,使得四边形ODCB是平行四边形,此时D点的坐标为(-2,-3),
当四边形OCBD是平行四边形时,D点即为A点,此时D点的坐标为(2,1)
(3)不存在.
如图2,由抛物线的对称性可知:AO=AB,∠AOB=∠ABO.
若△BOP与△AOB相似,必须有∠POB=∠BOA=∠BPO
设OP交抛物线的对称轴于A′点,显然A′(2,-1)
∴直线OP的解析式为y=-
| 1 |
| 2 |
由-
| 1 |
| 2 |
| 1 |
| 4 |

∴P(6,-3)
过P作PE⊥x轴,在Rt△BEP中,BE=2,PE=3,
∴PB=
| 13 |
∴PB≠OB,
∴∠BOP≠∠BPO,
∴△PBO与△BAO不相似,
同理可说明在对称轴左边的抛物线上也不存在符合条件的P点.
所以在该抛物线上不存在点P,使得△BOP与△AOB相似.
点评:本题考查了二次函数解析式的求法,利用抛物线的性质寻找平行四边形,相似三角形等问题,需要根据抛物线的对称性,形数结合,解答问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 轴上,CF交y轴于点B(0,2),且其面积为8.
轴上,CF交y轴于点B(0,2),且其面积为8.