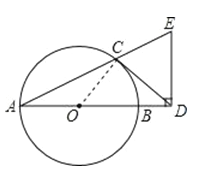
题目内容
【题目】已知,在![]() 中,
中,![]() ,点
,点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 重合).以
重合).以![]() 为边作正方形
为边作正方形![]() 连接
连接![]() .
.
观察猜想:
(1)如图1,当点![]() 在线段
在线段![]() 上时,判断
上时,判断![]() 之间数量关系,并证明;
之间数量关系,并证明;



类比探究:
(2)如图2,当点![]() 在线段
在线段![]() 的延长线上时,其他条件不变,请直接写出
的延长线上时,其他条件不变,请直接写出![]() 三条线段之间的关系;
三条线段之间的关系;
拓展延伸:
(3)如图3,当点![]() 在线段
在线段![]() 的反向延长线上时,且点
的反向延长线上时,且点![]() 分别在直线
分别在直线![]() 的两侧,其他条件不变;
的两侧,其他条件不变;
①请直接写出![]() 三条线段之间的关系;
三条线段之间的关系;
②若正方形![]() 的边长为
的边长为![]() 、对角线
、对角线![]() 相交于点
相交于点![]() ,连接
,连接![]() ,求
,求![]() 的长度.
的长度.
【答案】(1)![]() ;证明见解析;(2)
;证明见解析;(2)![]() ;(3)①
;(3)①![]() ,②
,② ![]() .
.
【解析】
(1)根据SAS证明△ABD≌△ACF,由△ABD≌△ACF的性质和线段的和可得结论;
(2)同理证明△ABD≌△ACF,可得BC⊥CF,由BD=BC+CD,BD=CF,可得新的结论:![]() ;
;
(3)①根据图3知:DC最长,同理:△DAB≌△FAC,则BD=CF,可得BC=DC-CF;
②先根据正方形的边长求对角线DF的长,证明∠DCF=90°,根据直角三角形斜边中线的性质可得OC的长.
证明:![]() ,
,![]() ,
,
![]()
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,
![]() ,
,![]()
![]()
则在![]() 和
和![]() 中,
中,

![]() ,
,
![]()
![]() ,
,
![]() ;
;
(2)证明:如图2,
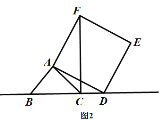
在正方形ADEF中,AD=AF,∠DAF=90°,
∵∠BAC=90°,
∴∠BAC+∠CAD=∠DAF+∠CAD,即∠BAD=∠CAF,
∵∠ABC=45°,
∴∠ACB=180°-∠BAC-∠ABC=45°,
∴∠ABC=∠ACB,
∴AB=AC,
在△ABD与△ACF中,

∴△ABD≌△ACF,
∴∠ACF=∠ABD=45°,BD=CF,
∵∠ACB=45°,
∴∠BCF=∠ACB+∠ACF=90°,
∴BC⊥CF;
∵BD=BC+CD,BD=CF,
∴![]() ;
;
(3)①理由是:如图3,
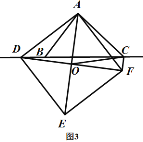
同理得:∠DAB=∠FAC,
与(2)同理,可证△DAB≌△FAC,
∴BD=CF,
∴DC=BD+BC=CF+BC,
∴BC=DC-CF;
![]() ,
,
![]()
![]()
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,
![]()
![]()
![]() 在
在![]() 和
和![]() 中,
中,

![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是直角三角形.
是直角三角形.
![]() 正方形
正方形![]() 的边长为
的边长为![]()
且对角线![]() 相交于点
相交于点![]()
![]()
![]() 为
为![]() 中点.
中点.
![]()