Question

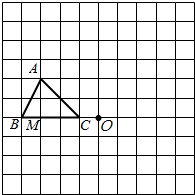在如图的方格纸中，每个小方格都是边长为1个单位的正方形，△ABC的三个顶点都在格点上（每个小方格的顶点叫格点）．
（1）画出△ABC向下平移4个单位后得到的△A₁B₁C₁；
（2）画出△ABC绕点O顺时针旋转90°后得到的△A₂B₂C₂，并标出点M旋转后的对应点M′的位置．
（3）求出线段MM′的长度．

Answer 1

分析：（1）由△ABC向下平移4个单位后得到的△A₁B₁C₁，根据平移的性质，即可求作出△A₁B₁C₁；
（2）由△ABC绕点O顺时针旋转90°后得到的△A₂B₂C₂，根据旋转的性质，即可作出△A₂B₂C₂，标出点M旋转后的对应点M′的位置；
（3）连接OM，OM′，MM′，可得∠MOM′=90°，OM=OM′=3，根据勾股定理，即可求得线段MM′的长度．

解答：解：（1）如图：△A₁B₁C₁；

（2）如图：△A₂B₂C₂；

（3）连接OM，OM′，MM′，

∵∠MOM′=90°，OM=OM′=3，
∴MM′=

OM2+OM′2

=3

2

．

点评：此题考查了平移与旋转的性质，考查了学生的动手能力．此题难度不大，解题的关键是注意数形结合思想的应用．