题目内容
 如图,在5×5的方格纸中,每一个小正方形的边长为1.
如图,在5×5的方格纸中,每一个小正方形的边长为1.
(1)∠BCD是不是直角?请说明理由(可以适当添加字母)
(2)求出四边形ABCD的面积;
(3)连接BD,求△ABD边AD上的高.
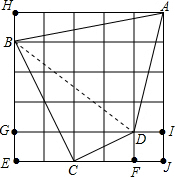 解:(1)∵BC2=CE2+BE2=22+42=20,CD2=CF2+DF2=12+22=5,BD2=GD2+BG2=32+42=25,(勾股定理)
解:(1)∵BC2=CE2+BE2=22+42=20,CD2=CF2+DF2=12+22=5,BD2=GD2+BG2=32+42=25,(勾股定理)∴BD2=BC2+CD2
根据勾股定理的逆定理可得∠BCD是直角.
(2)根据图示知,
S四边形ABCD=S正方形AHEJ-S△BCE-S△ABH-S△ADI-S△DCF-S正方形DFJI,
则S四边形ABCD=5×5-
 ×2×4-
×2×4- ×1×5-
×1×5- ×1×4-
×1×4- ×2×1-1×1=
×2×1-1×1=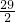 ,即四边形ABCD的面积是
,即四边形ABCD的面积是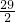 ;
;(3)设△ABD边AD上的高为h.
由(2)知,S四边形ABCD=
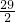 .
.根据图示知,S△ABD=S四边形ABCD-S△BCD,由(1)知,BD=5,BC=2
 ,CD=
,CD= ,
,则
 ×
× •h=
•h=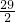 -
- ×
× ×2
×2 ,
,解得,h=
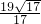 .
.所以,△ABD边AD上的高是
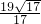 .
.分析:(1)连接BD,由于每一个小正方形的边长都为1,根据勾股定理可分别求出△BCD的三边长,根据勾股定理的逆定理即可判断出△BCD的形状.
(2)S四边形ABCD=S正方形AHEJ-S△BCE-S△ABH-S△ADI-S△DCF-S正方形DFJI;
(3)S△ABD=S四边形ABCD-S△BCD.
点评:本题考查了勾股定理、三角形的面积以及勾股定理的逆定理.解答(2)题时,采用了“分割法”来求不规则四边形ABCD的面积.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 3、如图,在8×4的方格(每个方格的边长为1个单位长)中,⊙A的半径为1,⊙B的半径为2,将⊙A由图示位置向右平移1个单位长后,⊙A与静止的⊙B的位置关系是( )
3、如图,在8×4的方格(每个方格的边长为1个单位长)中,⊙A的半径为1,⊙B的半径为2,将⊙A由图示位置向右平移1个单位长后,⊙A与静止的⊙B的位置关系是( )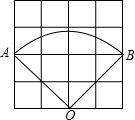 ,则扇形OAB周长等于
,则扇形OAB周长等于 如图,在8×4的方格(每个方格的边长为1个单位长)中,⊙A的半径为1,⊙B的半径为2,将⊙A由图示位置向右平移几个单位长度后与⊙B内切( )
如图,在8×4的方格(每个方格的边长为1个单位长)中,⊙A的半径为1,⊙B的半径为2,将⊙A由图示位置向右平移几个单位长度后与⊙B内切( ) 如图,在8×4的方格(每个方格的边长为1个单位长)中,⊙A的半径为l,⊙B的半径为2,将⊙A由图示位置向右平移1个单位长后,⊙A与静止的⊙B的位置关系是( )
如图,在8×4的方格(每个方格的边长为1个单位长)中,⊙A的半径为l,⊙B的半径为2,将⊙A由图示位置向右平移1个单位长后,⊙A与静止的⊙B的位置关系是( ) 如图,在10*10的方格纸中,有一个格点四边形ABCD(即四边形的顶点都在格点上),在给出的方格纸上,画出四边形ABCD关于直线L的对称的四边形A1B1C1D1.
如图,在10*10的方格纸中,有一个格点四边形ABCD(即四边形的顶点都在格点上),在给出的方格纸上,画出四边形ABCD关于直线L的对称的四边形A1B1C1D1.