题目内容
【题目】定义:点![]() 到图形
到图形![]() 上每一个点的距离的最小值称为点
上每一个点的距离的最小值称为点![]() 到图形
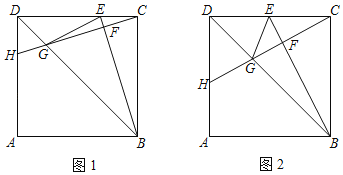
到图形![]() 的距离.例如,如图1,正方形
的距离.例如,如图1,正方形![]() 满足
满足![]() ,
,![]() ,
,![]() ,
,![]() ,那么点
,那么点![]() 到正方形
到正方形![]() 的距离为
的距离为![]() .
.

(1)如果点![]()
![]() 到抛物线
到抛物线![]() 的距离为
的距离为![]() ,请直接写出
,请直接写出![]() 的值________.
的值________.
(2)求点![]() 到直线
到直线![]() 的距离.
的距离.
(3)如果点![]() 在直线
在直线![]() 上运动,并且到直线
上运动,并且到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的坐标.
的坐标.
【答案】(1)b=-3;(2)![]() 到直线
到直线![]() 的距离为
的距离为![]() ;(3)(2, 6-
;(3)(2, 6-![]() )或
)或
(2, 6+![]() )
)
【解析】
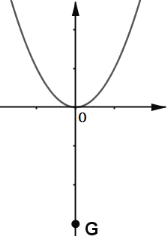
(1)作草图可知,当G在原点下方时,b=-3;
(2)过点M作直线y=x+3的垂线,与直线y=x+3相交于点H,则线段MH的长即为点M到直线y=x+3的距离.由等腰直角三角形MH=![]() ME求解即可;
ME求解即可;
(3)分N 在直线y=x+4的上方和下方求解即可.
解:(1)由图可知线段GO长即为点G到抛物线![]() 的距离,故GO=3,所以b=-3
的距离,故GO=3,所以b=-3
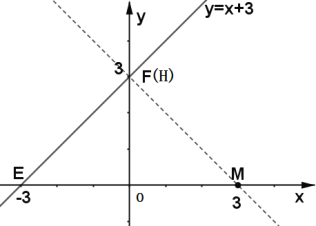
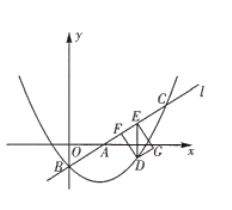
(2)如图,直线y=x+3与x,y轴分别交于点E(-3,0),F(0,3),直线y=x+3与x轴所成的角为45°,过点M作MH⊥EF,交EF与H,线段MH的长度即为点M到直线y=x+3的距离,且易知H点与F点重合.
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴EM=![]() FM ,
FM ,
又∵EF=3-(-3)=6,
∴MF=![]() EM=
EM=![]() ×6=3
×6=3![]()
∴MH=3![]()
即点![]() 到直线
到直线![]() 的距离为
的距离为![]() ;
;
(3)如图
K为直线x=2与x轴的交点,故K(2,0),F为直线x=2和直线y=x+4的交点,故F(2,6)
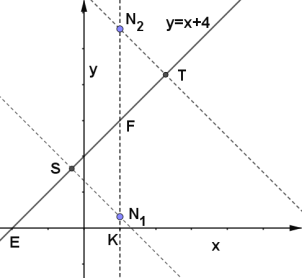
①当点N在直线y=x+4的下方N1处时,过点N1作N1S垂直直线y=x+4,
∵点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
∴SN1=4,
点E是直线y=x+4与x轴的交点,
∴E(-4,0),且∠FEK=45°,
∴![]() 为等腰直角三角形
为等腰直角三角形
∴EK=FK=2-(-4)=6,
F N1=![]() N1S=
N1S=![]() ,
,
∴KN1=FK- F N1=6-![]() ,
,
∴N1(2, 6-![]() )
)
②当点N在直线y=x+4的上方N2处时,过点N2作N2T垂直直线y=x+4,
同理可得:N2T=4,N2F= ![]() N2T=
N2T=![]() ,
,
∴N2K=KF+FN2=6+![]() ,
,
∴N2(2, 6+![]() )
)
故点![]() 在直线
在直线![]() 上运动,并且到直线
上运动,并且到直线![]() 的距离为
的距离为![]() ,
,![]() 的坐标为(2, 6-
的坐标为(2, 6-![]() )或
)或
(2, 6+![]() ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案