题目内容
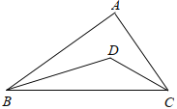
【题目】在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.选凉亭A,C作为观测点.如图,现测得∠CAB=45°,∠ACB=98°,AC=200米,请计算A,B两个凉亭之间的距离、(结果精确到1米)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,sin 37°≈0.6,cos 37°≈0.8,tan 37°≈0.75)
≈1.732,sin 37°≈0.6,cos 37°≈0.8,tan 37°≈0.75)
【答案】A,B两个凉亭之间的距离约为330米
【解析】
如下图,过点C作CH⊥BC交AB于点H,先在Rt△ACH中,求得AH的长,然后再Rt△BCH中,求得BH的长,从而得出AB的长.
解:过点C作CH⊥BC交AB于点H,
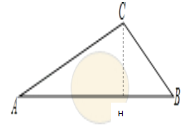
∵∠B=180°-∠CAB - ∠ACB=180°- 45°-98°=37°,
在Rt△ACH中,∠CAB=45°,AC=200米
∴CH=AC![]() sin∠CAB=200×
sin∠CAB=200×![]() =100
=100![]() ,
,
AH=AC![]() cos∠CAB=200×
cos∠CAB=200×![]() =100
=100![]()
在Rt△BCH中,∠B=37°,CH=100![]() 米
米
tan∠B=![]()
BH=![]() =
=![]()
∴AB=AH+BH=![]() ≈330
≈330
答:A,B两个凉亭之间的距离约为330米.

【题目】小明在“五一”假期间参加一项社会调查活动,在他所居住小区的600个家庭中,随机调查了50个家庭人均月收入情况,并绘制了如下的频数分布表和频数分布直方图(收入取整数,单位:元).
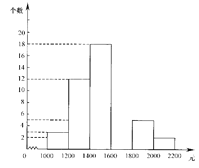
分 组 | 频 数 | 频 率 |
1000~1200 | 3 | 0.060 |
1200~1400 | 12 | 0.240 |
1400~1600 | 18 | 0.360 |
1600~1800 | 0.200 | |
1800~2000 | 5 | |
2000~2200 | 2 | 0.040 |
合计 | 50 | 1.000 |
请你根据以上提供的信息,解答下列问题:
⑴ 补全频数分布表和频数分布直方图;
⑵ 这50个家庭人均月收入的中位数落在 小组;
⑶ 请你估算该小区600个家庭中人均月收入较低(不足1400元)的家庭个数大约有多少?
【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的自变量
)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②
;②![]() 和3是关于
和3是关于![]() 的方程
的方程![]() 的两个根;③
的两个根;③![]()
![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3