题目内容
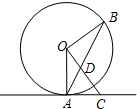 (2013•团风县模拟)已知:如图,点A、B在⊙O上,直线AC是⊙O的切线,连接AB交OC于点D,AC=CD.
(2013•团风县模拟)已知:如图,点A、B在⊙O上,直线AC是⊙O的切线,连接AB交OC于点D,AC=CD.(1)求证:OC⊥OB;
(2)如果OD=1,tan∠OCA=
| ||
| 2 |
分析:(1)根据OB=OA求出∠B=∠4,根据AC=CD得出∠1=∠2=∠3,根据切线性质求出∠1+∠4=90°=∠B+∠3,求出∠BOD度数即可;
(2)根据锐角三角函数得出OA:AC=2:
,设AC=2x,则AO=
x,由勾股定理求出OC=3x,得出3x=2x+1,求出x即可.
(2)根据锐角三角函数得出OA:AC=2:
| 5 |
| 5 |
解答: (1)证明:
(1)证明:
∵OA=OB,
∴∠B=∠4.
∵CD=AC,
∴∠1=∠2.
∵∠3=∠2,
∴∠3=∠1.
∵AC是⊙O的切线,
∴OA⊥AC,
∴∠OAC=90°,
∴∠1+∠4=90°,
∴∠3+∠B=90°,
∴∠BOD=90°,
∴OC⊥OB,
解:(2)在Rt△OAC中,∠OAC=90°,
∵tan∠OCA=
,
∴
=
,
∴设AC=2x,则AO=
x,
由勾股定理得,OC=3x.
∵AC=CD,
∴AC=CD=2x.
∵OD=1,
∴OC=2x+1.
∴2x+1=3x,
∴x=1,
∴AC=2×1=2.
 (1)证明:
(1)证明:∵OA=OB,
∴∠B=∠4.
∵CD=AC,
∴∠1=∠2.
∵∠3=∠2,
∴∠3=∠1.
∵AC是⊙O的切线,
∴OA⊥AC,
∴∠OAC=90°,
∴∠1+∠4=90°,
∴∠3+∠B=90°,
∴∠BOD=90°,
∴OC⊥OB,
解:(2)在Rt△OAC中,∠OAC=90°,
∵tan∠OCA=
| ||
| 2 |
∴
| OA |
| AC |
| ||
| 2 |
∴设AC=2x,则AO=
| 5 |
由勾股定理得,OC=3x.
∵AC=CD,
∴AC=CD=2x.
∵OD=1,
∴OC=2x+1.
∴2x+1=3x,
∴x=1,
∴AC=2×1=2.
点评:本题考查了勾股定理,切线的性质,等腰三角形的性质,三角形的内角和定理等知识点,主要考查学生综合运用性质进行推理和计算的能力,题目比较好,综合性比较强.

练习册系列答案
相关题目
 (2013•团风县模拟)由一些大小相同的小正方形搭成的一个几何体的三视图如图所示,则构成这个几何体的小正方体共有( )
(2013•团风县模拟)由一些大小相同的小正方形搭成的一个几何体的三视图如图所示,则构成这个几何体的小正方体共有( )