题目内容
如图，⊙O1和⊙O2的半径分别为1和3，连接O1O2，交⊙O2于点P，已知O1O2=8，若将⊙O1绕点P按顺时针方向旋转360°，则⊙O1与⊙O2共相切（ ）分析：根据两圆相切时，O1O2之间的距离等于4（外切）或者2（内切）时即可，分别得出当⊙O1绕P点顺时针旋转时360°时，O1O2的变化范围从8到2再到8，其中有两次外切和一次内切．
解答：解：两圆相切时，O1O2之间的距离等于4（外切）或者2（内切）时即可，
当⊙O1绕P点顺时针旋转时360°时，O1O2的变化范围从8到2再到8，其中有两次外切和一次内切．可以用尺规作图的方法来做，以P为圆心做一个半径为5的圆，再以O2为圆心，做一个半径为4的圆，两者相交即为外切，
然后以O2为圆心做一个半径为2的圆，两者相交即为内切．
故⊙O1与⊙O2共相切3次．
故选D．
当⊙O1绕P点顺时针旋转时360°时，O1O2的变化范围从8到2再到8，其中有两次外切和一次内切．可以用尺规作图的方法来做，以P为圆心做一个半径为5的圆，再以O2为圆心，做一个半径为4的圆，两者相交即为外切，
然后以O2为圆心做一个半径为2的圆，两者相交即为内切．
故⊙O1与⊙O2共相切3次．
故选D．
点评：此题主要考查了圆与圆的位置关系，得出当⊙O1绕P点顺时针旋转时360°时，O1O2的变化范围从8到2再到8，其中有两次外切和一次内切是解决问题的关键．
练习册系列答案
相关题目
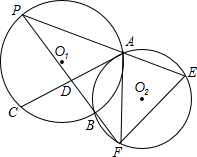
20、已知：如图，⊙O1和⊙O2相交于A、B两点，动点P在⊙O2上，且在⊙1外，直线PA、PB分别交⊙O1于C、D，问：⊙O1的弦CD的长是否随点P的运动而发生变化？如果发生变化，请你确定CD最长和最短时P的位置，如果不发生变化，请你给出证明．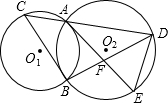
长⊙O1相交于C点，连接BC，过A点作AE∥BC与⊙O相交于E点，与BD相交于F点．
、PB的延长线分别交⊙O2于点E、F，PB交AC于D．
16、如图．⊙O1和⊙O2外切于点A，BC是⊙O1和⊙O2的公切线，B、C为切点，求证：AB⊥AC．
（2001•黄冈）已知，如图，⊙O1和⊙O2内切于点P，过点P的直线交⊙O1于点D，交⊙O2于点E；DA与⊙O2相切，切点为C．