题目内容
16、如图．⊙O1和⊙O2外切于点A，BC是⊙O1和⊙O2的公切线，B、C为切点，求证：AB⊥AC．分析：作两圆的内公切线MN，交BC于点D，根据切线长定理和直角三角形的判定方方法进行证明．
解答：
证明：作两圆的内公切线MN；
∵MN是⊙O1和⊙O2的公切线，交BC于点D，
∴AD=BD，AD=CD；
∴AD=BD=CD．
∴AC⊥AB．
证明：作两圆的内公切线MN；∵MN是⊙O1和⊙O2的公切线，交BC于点D，
∴AD=BD，AD=CD；
∴AD=BD=CD．
∴AC⊥AB．
点评：掌握切线长定理和直角三角形的判定方法．作两圆的内公切线是两圆中常见的一条辅助线．
练习册系列答案
相关题目
20、已知：如图，⊙O1和⊙O2相交于A、B两点，动点P在⊙O2上，且在⊙1外，直线PA、PB分别交⊙O1于C、D，问：⊙O1的弦CD的长是否随点P的运动而发生变化？如果发生变化，请你确定CD最长和最短时P的位置，如果不发生变化，请你给出证明．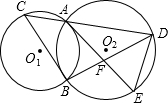
长⊙O1相交于C点，连接BC，过A点作AE∥BC与⊙O相交于E点，与BD相交于F点．
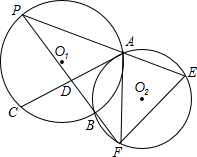、PB的延长线分别交⊙O2于点E、F，PB交AC于D．
（2001•黄冈）已知，如图，⊙O1和⊙O2内切于点P，过点P的直线交⊙O1于点D，交⊙O2于点E；DA与⊙O2相切，切点为C．