题目内容
已知：如图，⊙O1和⊙O2相交于A、B两点，过B点作⊙O1的切线交⊙O2于D点，连接DA并延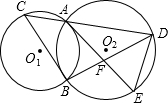
长⊙O1相交于C点，连接BC，过A点作AE∥BC与⊙O相交于E点，与BD相交于F点．（1）求证：EF•BC=DE•AC；
（2）若AD=3，AC=1，AF=
| 3 |
分析：（1）连接AB，证明△ACB∽△FED，根据相似三角形的性质，可得EF•BC=DE•AC；
（2）先证出△AFB∽△BAC，利用相似三角形的性质，得
=
，可求出AB的长；连接BE，利用△ACB∽△EBD，利用相似三角形的性质，可得
=
，可求出DE的长，再将所求数据代入EF•BC=DE•AC；便可求出EF的长．
（2）先证出△AFB∽△BAC，利用相似三角形的性质，得
| AF |
| AB |
| AB |
| BC |
| AB |
| DE |
| CB |
| DB |
解答：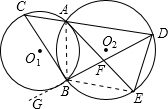
（1）证明：连接AB，切线DB另一端为G
∵BD是切线
∴∠ABD=∠ACB，∠CBG=∠CAB
∵∠ABD=∠DEF
∴∠ACB=∠DEF
∵AE∥BC
∴∠CBG=∠AFB
∵∠AFB=∠DFE
∴∠CAB=∠DFE
∴△ABC∽△FDE
∴
=
∴EF•BC=DE•AC；
（2）解：∵CB∥AE，
∴
=
，
∴
=
，
∴CB=
，
∵BD为⊙O1的切线，
∴∠ABD=∠C，
又∵CB∥AE，
∴∠ABC=∠BAF，
∴△AFB∽△BAC，
∴
=
，
∴AB2=AF•BC=
×
=4，
∴AB=2．
又∵DB2=AD•CD，
∴DB=
=2
，
连接BE，∴△ACB∽△EBD，
∴
=
，
∴
=
，
∴DE=3．
∵EF•BC=DE•AC，
∴EF•
=3×1，
∴EF=
．
（1）证明：连接AB，切线DB另一端为G∵BD是切线
∴∠ABD=∠ACB，∠CBG=∠CAB
∵∠ABD=∠DEF
∴∠ACB=∠DEF
∵AE∥BC
∴∠CBG=∠AFB
∵∠AFB=∠DFE
∴∠CAB=∠DFE
∴△ABC∽△FDE
∴
| BC |
| DE |
| AC |
| EF |
∴EF•BC=DE•AC；
（2）解：∵CB∥AE，
∴
| AD |
| DC |
| AF |
| CB |
∴
| 3 |
| 4 |
| ||
| CB |
∴CB=
4
| ||
| 3 |
∵BD为⊙O1的切线，
∴∠ABD=∠C，
又∵CB∥AE，
∴∠ABC=∠BAF，
∴△AFB∽△BAC，
∴
| AF |
| AB |
| AB |
| BC |
∴AB2=AF•BC=
| 3 |
4
| ||
| 3 |
∴AB=2．
又∵DB2=AD•CD，
∴DB=
| 3×4 |
| 3 |
连接BE，∴△ACB∽△EBD，
∴
| AB |
| DE |
| CB |
| DB |
∴
| 2 |
| DE |
| ||||
2
|
∴DE=3．
∵EF•BC=DE•AC，
∴EF•
4
| ||
| 3 |
∴EF=
3
| ||
| 4 |
点评：本题不仅考查了和圆相关的相似三角形的性质，还考查了切割线定理、圆内接四边形的性质等知识，有一定的难度．
练习册系列答案
相关题目
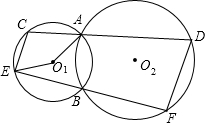已知：如图，⊙O1和⊙O2相交于A、B两点，经过A的直线CD与⊙O1交于点C、与⊙O2交于点D，经过点B的直线EF与⊙O1交于点E、与⊙O2交于点F，连接CE、DF．若∠AO1E=100°，则∠D的度数为
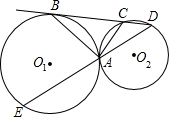O1于点E．
20、已知：如图，⊙O1和⊙O2相交于A、B两点，动点P在⊙O2上，且在⊙1外，直线PA、PB分别交⊙O1于C、D，问：⊙O1的弦CD的长是否随点P的运动而发生变化？如果发生变化，请你确定CD最长和最短时P的位置，如果不发生变化，请你给出证明．
（2001•黄冈）已知，如图，⊙O1和⊙O2内切于点P，过点P的直线交⊙O1于点D，交⊙O2于点E；DA与⊙O2相切，切点为C．