题目内容
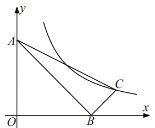
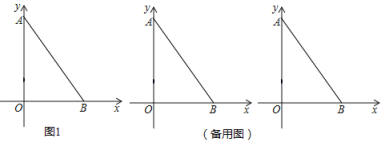
【题目】如图1,平面直角坐标系中,A(0,8)、B(6,0) .动点P从A点出发,沿y轴负半轴方向运动,速度每秒2个单位长度,动点Q从B点出发,沿BA方向向A点运动,速度每秒1个单位长度.两点同时出发,Q点到达A点时,两点同时停止运动,运动时间为t秒.
(1)当△APQ面积为12,求t的值.
(2)当△APQ的外心(三角形的外心是三角形三边垂直平分线的交点)在△APQ的边上时,求t值.
(3)若Q点在直线AB上运动,过Q点作QH⊥x轴,垂足为H,当△QBH与△ABO的相似比为1:2时,直接写出Q点坐标.
【答案】(1)5+![]() 或5-
或5-![]() ;(2)
;(2) ![]() 或
或![]() ;(3)(3,4)或(9,-4)
;(3)(3,4)或(9,-4)
【解析】
(1)作QC⊥OB于点C,根据平行线分线段成比例定理求出OC的长,然后根据三角形的面积公式列方程求解即可;
(2)由△APQ的外心在△APQ的边上可知△APQ 是直角三角形,分∠APQ=90°和∠AQP=90°两种情况求解即可;
(3)分点Q在线段AB上和射线AB上两种情况求解即可.
(1)如图1,作QC⊥OB于点C,则QC∥OA,
由题意得,AP=2t,BQ=t,AB=![]() ,AQ=10-t,
,AQ=10-t,
∵QC∥OA,
∴![]() ,
,
∴![]() ,
,
∴OC=![]() ,
,
∴![]() ,
,
解之得t1=5+![]() ,t2=5-
,t2=5-![]() ,
,
∴t的值是5+![]() 或5-
或5-![]() ;
;
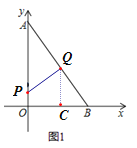
(2)∵△APQ的外心在△APQ的边上,
∴△APQ的是直角三角形,
如图2,当∠APQ=90°时,则PQ∥OB,
∴![]() ,
,
∴![]() ,
,
解之得:t=![]() ;
;
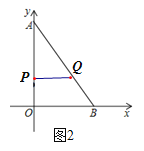
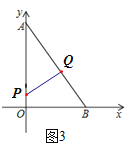
如图3,当∠AQP=90°时,
∵![]() ,
,
∴![]() ,
,
解之得:t=![]() .
.
∴t的值是![]() 或
或![]() ;
;
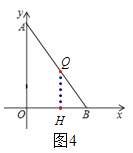
(3)如图4,当点Q在线段AB上时,
∵QH⊥OB,AO⊥OB,
∴△QBH∽△ABO,
∴![]() ,
,
∴![]() ,
,
∴BH=3,QH=4,
∴OH=6-3=3,
∴Q(3,4);
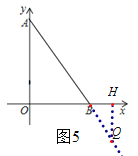
如图5,当点Q在射线AB上时,同理可求Q(9,-4).
∴Q点坐标(3,4)或(9,-4).

 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案