题目内容
【题目】(1)如图①,画一条平行于BC的直线,使其将△ABC分成两部分,且所分三角形与梯形面积比为1:3;
(2)如图②,△ABC中AB=4,AC=3,BC=6,D是△ABC中AC边上的点,AD=2,过点D画一条直线l将△ABC分成两部分,l与△ABC另一边的交点为点P,使其所分的一个三角形与△ABC相似,并求出DP的长;
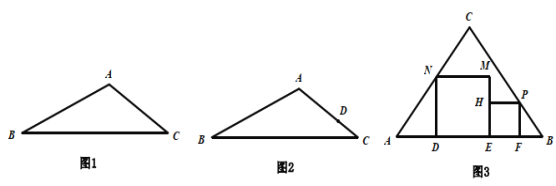
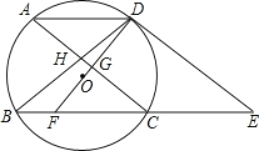
(3)如图③所示,在等腰△ABC中,CA=CB=10,AB=12.在△ABC中放入正方形DEMN和正方形EFPH,使得DE.EF在边AB上,点P.N分别在边CB.CA上,若较大正方形的边长为a,请用含a的代数式表示较小正方形的边长.
【答案】(1)见解析;(2)见解析,PD=4;(3)小正方形边长为![]() .
.
【解析】
(1)直线MN将三角形与梯形面积比为1:3,则△AMN与△ABC的面积比是1:4,则相似比是1:2,所以过AB,AC的中点M,N作BC的平行线即可;
(2)先求到CD=1,再分DP// BC,DP//AB,∠CDP=∠B, ∠ADP=∠B四种情况讨论,可得到DP的长;
(3)设正方形EFPH的边长为b,过点C作CG⊥AB于点G,证得△ADN∽△AGC,△BFP∽△BGC,得到![]() ,
,![]() ,再根据AD+DE +EF +FB=AB=12,所以
,再根据AD+DE +EF +FB=AB=12,所以![]() ,从而得到小正方形边长为
,从而得到小正方形边长为![]() .
.
解: (1)如图所示:直线MN即为所求,M.N分别为AB.AC中点
(2)∵AC=3, AD=2,
∴ CD=1
①当DP// BC时,△APD∽△ABC
![]() ,即
,即![]()
∴ PD=4
②当DP//AB时,△CDP∽△CAB
![]() ,即
,即![]()
![]()
③当∠CDP=∠B时,△CDP∽△CBA
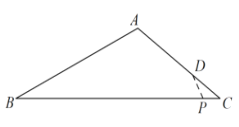
![]() ,即
,即![]()
∴ ![]()
④当∠ADP=∠B时,,则△ADP∽△ABC,
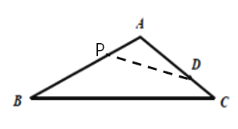
![]() ,即
,即![]()
∴ ![]()
(3)设正方形EFPH的边长为b,过点C作CG⊥AB于点G,
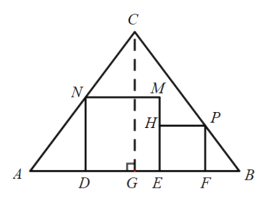
∵CA=CB=10, AB=12
∴ AG=BG=6
在Rt△AGC中,由勾股定理,得:
![]()
由题意得: △ADN∽△AGC,△BFP∽△BGC
![]() ,
,![]()
即![]() ,
,![]()
∴ ![]() ,
,![]()
∵AD+DE +EF +FB=12
∴![]() ,即a+b=
,即a+b=![]()
∴ ![]()
综上所述,小正方形边长为![]()

【题目】抛物线![]() 上部分点的横坐标x纵坐标y的对应值如下表
上部分点的横坐标x纵坐标y的对应值如下表
x |
|
|
| 0 | 1 | 2 |
|
y |
| 0 |
|
| 0 | 8 |
|
![]() 写出该抛物线的对称轴及当
写出该抛物线的对称轴及当![]() 时对应的函数值;
时对应的函数值;
![]() 求出抛物线
求出抛物线![]() 的解析式,并在平面直角坐标系中画出该抛物线的图象;
的解析式,并在平面直角坐标系中画出该抛物线的图象;
(3)结合图象回答:
①不等式![]() 的解集是___________________;
的解集是___________________;
②当![]() 时,y的取值范围是__________________.
时,y的取值范围是__________________.