题目内容
【题目】阅读下面材料
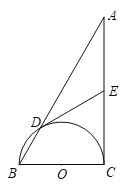
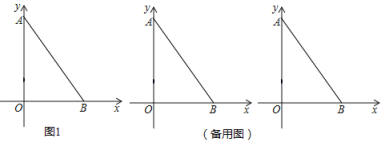
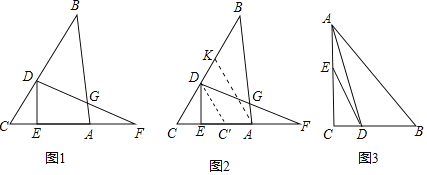
小胖同学遇到这样一个问题:如图1,△ABC中,点D在BC上,点F是CA延长线上的点,连接DF交AB于G.过点D作DE⊥AC,垂足为E.若∠AGD=2∠C,DF=AB,求![]() 的值.
的值.
小胖通过计算角度发现∠BGD=2∠CDE,于是作出点C关于DE的对称点C′,使得∠CDC′=∠BGD,进而得出∠C′DF=∠B,接着截取BK=DC,得出一组全等三角形.
(1)请沿着小胖的思路继续完成此题的解答过程:
(2)参考小胖的解题方法完成下面问题:
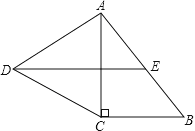
如图3,在△ABC中,∠ACB=2∠B,BD=2CD,∠BAD=∠CED,探索AE、CE、CD三条线段的数量关系.
【答案】(1)![]() ;(2)AE=CE﹣CD.
;(2)AE=CE﹣CD.
【解析】
(1)根据SAS可证明△ABK≌△FDC',得出AK=FC',∠AKB=∠FC'D,证明CE=C′E,则可求出![]() ;
;
(2)作∠BDF=∠B交AB于F点,延长BC到G点,使得CG=CA,证明△CED∽△FAD,得出比例线段![]() ,设CD=x,BD=2x,CE=y,可得出DG=2y,则CG=AC=DG=2y-x,可得出AE=y-x=CE-CD.
,设CD=x,BD=2x,CE=y,可得出DG=2y,则CG=AC=DG=2y-x,可得出AE=y-x=CE-CD.
(1)∵BK=CD=C′D,∠C′DF=∠B,DF=AB,
∴△ABK≌△FDC'(SAS),
∴AK=FC',∠AKB=∠FC'D,
∴∠C=∠AKC,
∴AK=AC=FC′,
∵DE⊥CC',且DC=DC',
∴CE=C′E,
∴AF=2CE,
∴![]() ;
;
(2)AE=CE﹣CD.
如图,作∠BDF=∠B交AB于F点,延长BC到G点,使得CG=CA,
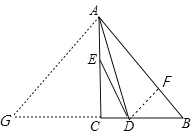
∴DF=FB,
∴∠FDB=∠B,
∴∠G=∠CAG=∠B=∠FDB,
∴DF∥AG,∠ECD=2∠B,
∴∠AFD=∠ECD,∠CED=∠FAD,
∴△CED∽△FAD,
∴![]() ,
,
设CD=x,BD=2x,CE=y,
∴![]() ,
,
∴![]() ,
,
∴DG=2y,
∴CG=AC=DG﹣CD=2y﹣x,
∴AE=AC﹣CE=y﹣x=CE﹣CD.

 53随堂测系列答案
53随堂测系列答案