Question

【题目】（定义）若一个四边形恰好关于其中一条对角线所在的直线对称，则我们将这个四边形叫做镜面四边形．

（理解）（1）下列说法是否正确（对的打√，错的打×）

①平行四边形是一个镜面四边形　 　

②镜面四边形的面积等于对角线积的一半．　 　

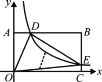
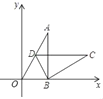
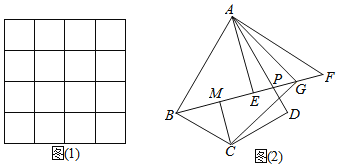
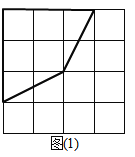
（2）如图（1），请你在4×4的网格（每个小正方形的边长为1）中画出一个镜面四边形，使它图（1）的顶点在格点上，且有一边长为．

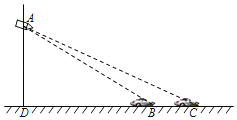
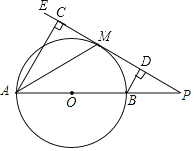
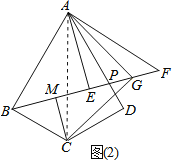
（应用）（3）如图（2），已知镜面四边形ABCD，∠BAD＝60°，∠ABC＝90°，AB≠BC，P是AD上一点，AE⊥BP的延长线上取一点F，使EF＝BE，连接AF，作∠FAD的平分线AG交BF于G，CM⊥BF于M，连接CG．

①求∠EAG的度数．

②比较BM与EG的大小，并说明理由．

Answer 1

【答案】（1）①×；②√；（2）见解析；（3）①30°；②BM＝EG，见解析

【解析】

（1）根据平行四边形的性质和镜面四边形的定义，直接判断；

（2）由镜面四边形的意义，得到必有两边是，一个直角，画出图形即可

（3）①根据角平分线的定义得到∠EAF＝∠BAF，∠GAF＝∠FAD计算；②先判断△ABE∽△BCM，通过计算判断出BM＝EG

解：（1）①∵平行四边形不一定关于任何一条对角线对称，

∴错误，

故答案×；

②∵镜面四边形关于对角线对称，

∴镜面四边形的两条对角线互相垂直，

∴镜面四边形的面积等于对角线积的一半；

故答案为√．

（2）∵有一边长为．

∴镜面四边形必有两边是．

如图（1）

（3）①∵AE⊥BP，EF＝BE，

∴AB＝AF，

∴∠EAF＝∠BAF，

∵∠GAF＝∠FAD，

∴∠EAG＝∠EAF﹣∠GAF＝∠BAF﹣∠FAD＝∠BAD＝30°；

②BM＝EG，

理由如下：如图（2）连接AC，

∵∠ABC＝90°，∠BAD＝60°，

∴AB＝BC，

∵∠ABC＝∠AEB＝∠CMB＝90°，

∴∠BAE+∠ABF＝∠ABP+∠ABF＝90°，

∴∠BAE＝∠CBF，

∴△ABE∽△BCM，

∴，

∴AE＝BM，

∵∠EAG＝30°，AE⊥BP，

∴AE＝EG，

∴BM＝EG．