题目内容
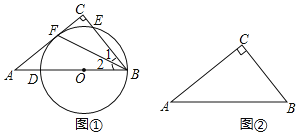
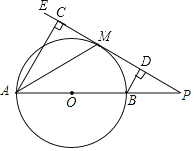
【题目】如图,AB为⊙O的直径,点P为AB延长线上的一点,过点P作⊙O的切线PE,切点为M,过A、B两点分别作PE的垂线AC、BD,垂足分别为C、D,连接AM,则下列结论正确的是___________.(写出所有正确结论的序号)
①AM平分∠CAB;
②AM2=ACAB;
③若AB=4,∠APE=30°,则![]() 的长为
的长为![]() ;
;
④若AC=3,BD=1,则有CM=DM=![]() .
.
【答案】①②④
【解析】
连接OM,由切线的性质可得OM⊥PC,继而得OM∥AC,再根据平行线的性质以及等边对等角即可求得∠CAM=∠OAM,由此可判断①;通过证明△ACM∽△AMB,根据相似三角形的对应边成比例可判断②;求出∠MOP=60°,利用弧长公式求得![]() 的长可判断③;由BD⊥PC,AC⊥PC,OM⊥PC,可得BD∥AC//OM,继而可得PB=OB=AO,PD=DM=CM,进而有OM=2BD=2,在Rt△PBD中,PB=BO=OM=2,利用勾股定理求出PD的长,可得CM=DM=DP=
的长可判断③;由BD⊥PC,AC⊥PC,OM⊥PC,可得BD∥AC//OM,继而可得PB=OB=AO,PD=DM=CM,进而有OM=2BD=2,在Rt△PBD中,PB=BO=OM=2,利用勾股定理求出PD的长,可得CM=DM=DP=![]() ,由此可判断④.
,由此可判断④.
连接OM,

∵PE为⊙O的切线,
∴OM⊥PC,
∵AC⊥PC,
∴OM∥AC,
∴∠CAM=∠AMO,
∵OA=OM,
∠OAM=∠AMO,
∴∠CAM=∠OAM,即AM平分∠CAB,故①正确;
∵AB为⊙O的直径,
∴∠AMB=90°,
∵∠CAM=∠MAB,∠ACM=∠AMB,
∴△ACM∽△AMB,
∴![]() ,
,
∴AM2=ACAB,故②正确;
∵∠APE=30°,
∴∠MOP=∠OMP﹣∠APE=90°﹣30°=60°,
∵AB=4,
∴OB=2,
∴![]() 的长为
的长为![]() ,故③错误;
,故③错误;
∵BD⊥PC,AC⊥PC,OM⊥PC,
∴BD∥AC//OM,
∴△PBD∽△PAC,
∴![]() ,
,
∴PB=![]() PA,
PA,
又∵AO=BO,AO+BO=AB,AB+PB=PA,
∴PB=OB=AO,
又∵BD∥AC//OM,
∴PD=DM=CM,
∴OM=2BD=2,
在Rt△PBD中,PB=BO=OM=2
∴PD=![]() =
=![]() ,
,
∴CM=DM=DP=![]() ,故④正确,
,故④正确,
故答案为:①②④.

 阅读快车系列答案
阅读快车系列答案