Question

【题目】如图，抛物线y=﹣x2﹣x+与x轴交于A、B两点（点A在点B左侧），与y轴交于点C．

（1）求该抛物线的对称轴和线段AB的长；

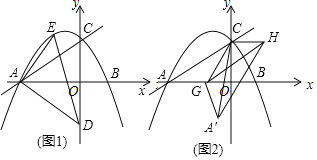
（2）如图1，已知点D（0，﹣），点E是直线AC上访抛物线上的一动点，求△AED的面积的最大值；

（3）如图2，点G是线段AB上的一动点，点H在第一象限，AC∥GH，AC=GH，△ACG与△A′CG关于直线CG对称，是否存在点G，使得△A′CH是直角三角形？若存在，请直接写出点G的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）AB=4，抛物线的对称轴x=﹣1；（2）m=﹣时，S△AED有最大值，最大值为；（3）满足条件点G坐标为（﹣1，0）或（0，0）或（1，0）．

【解析】

（1）利用待定系数法即可解决问题；
（2）如图1中，设E（m，﹣m2﹣m+），根据S△AED=S△AOD+S△AEO+S△ECO-S△ECD根据二次函数，利用二次函数的性质即可解决问题；
（3）分三种情形①如图2中，连接BC．当点A′在y轴上时，∠HCA′=90°满足条件．②如图3中，当点G与点O重合时，易证四边形GCHA′是矩形，此时△CHA′是直角三角形；③如图4中，当点G与B重合时，四边形GCHA′是矩形，此时△CHA′是直角三角形.

解：（1）对于y=﹣x2﹣x+令y=0，可得﹣x2﹣x+=0，

解得x=﹣3或1，

∴A（﹣3，0），B（1，0），

∴AB=4，

抛物线的对称轴x=﹣=﹣=﹣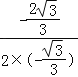1．

（2）如图1中，设E（m，﹣m2﹣m+），

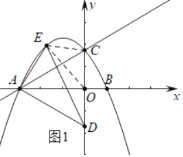
∵S△AED=S△AOD+S△AEO+S△ECO﹣S△ECD

=×3×+×3×（﹣m2﹣m+）+××（﹣m）﹣×2×（﹣m）

=﹣（m+）2+，

∵﹣＜0，

∴m=﹣时，S△AED有最大值，最大值为．

（3）①如图2中，连接BC．

∵AC∥GH，AC=GH，

∴四边形ACHG是平行四边形，

∴CH∥AB，

当点A′在y轴上时，∠HCA′=90°满足条件．

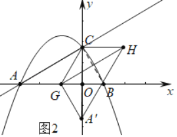
∵AO=3，OC=，OB=1，

∴tan∠CAO==，tan∠BCO==，

∴∠CAO=30°，∠OCB=30°，

∴∠ACO=60°，

∴∠ACB=∠ACO+∠OCB=90°，

当点A′在y轴上时，∠ACG=∠A′CG=30°，

∴OG=OCtan30°=1，

∴G（﹣1，0）．

②如图3中，当点G与点O重合时，易证四边形GCHA′是矩形，此时△CHA′是直角三角形；

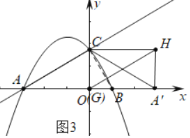
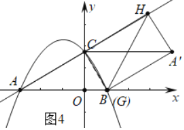
③如图4中，当点G与B重合时，四边形GCHA′是矩形，此时△CHA′是直角三角形，G（1，0），

综上所述，满足条件点G坐标为（﹣1，0）或（0，0）或（1，0）．