Question

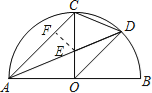
【题目】如图，AB是半圆直径，半径OC⊥AB于点O，AD平分∠CAB交弧BC于点D，连结CD、OD，给出以下四个结论：①AC∥OD；②CE=OE；③△ODE∽△ADO；④．其中正确结论的序号是（　）

A. 1个 B. 2个 C. 3个 D. 4个

Answer 1

【答案】B

【解析】

①∵AB是半圆直径，∴AO=OD，∴∠OAD=∠ADO，

∵AD平分∠CAB交弧BC于点D，∴∠CAD=∠DAO=∠CAB，∴∠CAD=∠ADO，

∴AC∥OD，∴①正确．

②过点E作EF⊥AC，∵OC⊥AB，AD平分∠CAB交弧BC于点D，∴OE=EF，

在Rt△EFC中，CE＞EF，∴CE＞OE，∴②错误．

③∵在△ODE和△ADO中，只有∠ADO=∠EDO，∵∠COD=2∠CAD=2∠OAD，

∴∠DOE≠∠DAO，∴不能证明△ODE和△ADO相似，∴③错误；

④∵AD平分∠CAB交弧BC于点D，∴∠CAD=×45°=22.5°，∴∠COD=45°，

∵AB是半圆直径，∴OC=OD，∴∠OCD=∠ODC=67.5°∵∠CAD=∠ADO=22.5°（已证），

∴∠CDE=∠ODC-∠ADO=67.5°-22.5°=45°，∴△CED∽△COD，∴，

∴CD2=ODCE=ABCE，∴2CD2=CEAB．∴④正确．综上所述，只有①④正确．故选B．