题目内容
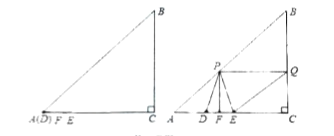
【题目】如图⊙O的内接△ABC中,外角∠ACF的角平分线与⊙O相交于D点,DP⊥AC,垂足为P,DH⊥BF,垂足为H.问:
(1)∠PDC与∠HDC是否相等,为什么?
(2)图中有哪几组相等的线段?
(3)当△ABC满足什么条件时,△CPD∽△CBA,为什么?

【答案】(1)相等,理由详见解析;(2)PC=HC,DP=DH,AP=BH,AD=BD;(3)∠ABC=90°且∠ACB=60°时,△CPD∽△CBA.
【解析】
(1)根据“AAS”证明△CDH≌△CDP即可;
(2)发现全等三角形,根据全等三角形的对应边相等证明出线段相等;
(3)根据其中一个是直角三角形得到AC必须是直径.再根据另一对角对应相等,结合利用平角发现∠PCD=∠DCF=∠ACB=60°才可.
解 (1)相等.理由如下:
∵CD为∠ACF的角平分线(已知),
∴∠DCP=∠DCH,
∵DP⊥AC,DH⊥BF.
∴∠DPC=∠DHC=90°,
又∵CD=CD,
∴△CDH≌△CDP,
∴∠PDC=∠HDC.
(2) ∵△CDH≌△CDP,
∴PC=HC,DP=DH,
∵∠DAP=∠DBH,∠APD=∠BHD=90°,
∴△ADP≌△BDH,
∴AP=BH,AD=BD.
综上可得:PC=HC,DP=DH,AP=BH,AD=BD.
(3)∠ABC=90°且∠ACB=60°时,△CPD∽△CBA.
∵∠CPD=90°,
∴∠ABC=90°.
∵CD为∠ACF的角平分线,∠PCD=∠DCF=∠ACB,
∴∠ACB=60°.
∴∠ABC=90°且∠ACB=60°时,△CPD∽△CBA.

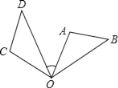
【题目】如图,将△OAB绕点O逆时针旋转80°得到△OCD,点A与点C是对应点.
(1)画出△OAB关于点O对称的图形(保留画图痕迹,不写画法);
(2)若∠A=110°,∠D=40°,求∠AOD的度数.