题目内容
【题目】如图,将正方形网格放置在平面直角坐标系中,其中每个小正方形的边长均为1,△ABC经过平移后得到△A1B1C1,若AC上一点P(1.2,1.4)平移后对应点为P1,点P1绕原点顺时针旋转180°,对应点为P2,则点P2的坐标为( )
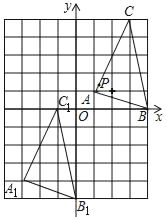
A. (2.8,3.6) B. (﹣2.8,﹣3.6)
C. (3.8,2.6) D. (﹣3.8,﹣2.6)
【答案】A
【解析】
根据平移的性质得出,△ABC的平移方向以及平移距离,即可得出P1坐标,进而利用中心对称图形的性质得出P2点的坐标.
∵A点坐标为:(1,1),A1(-3,-4),
∴△ABC向左平移了4个单位,向下平移了5个单位,
∴点P(1.2,1.4)平移后的对应点P1为:(-2.8,-3.6),
∵点P1绕点O逆时针旋转180°,得到对应点P2,
∴P2点的坐标为:(2.8,3.6).
故选A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
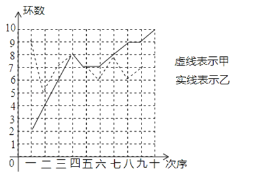
【题目】甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
(1)请填写下表:
平均数 | 方差 | 中位数 | 命中9环以上(包括9环)次数 | |
甲 | 7 |
|
|
|
乙 |
| 5.4 |
|
|
(2)请你就下列两个不同的角度对这次测试结果进行
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和命中9环(包括9环)以上次数相结合看(分析谁的潜能更大).